This problem was started by James in Help Me Board and is quite a challenge and has inspired previous 2 posts by me here and now a 3rd post.
Containing a bouncing circle inside a raggedy frame of random line segments, the problem arises, for me, of overcoming "stuck" points where the circle runs into a segment corner (called peninsulas by me) here the circle center may be clear of corner but it's lower body gets stuck pressing into corner.
First how to detect stick points in code?
2nd how to escape them?
To detect a stick, I just check the new coordinates of circle x, y if neither of them has changed, it's stuck.
If I find that condition then I change the ball angle to the perpendicular of the line segment (blue color code) it's mostly stuck at instead of using it's natural reflective angle (white color code). This seems to get the ball clear most every time.
There are times when ball gets wedged into a "bay" and this method of getting unstuck doesn't look like it would help much, the white arrow looks like the best way out but using the perpendicular doesn't seem to get it stuck worse...
See for yourself, let this demo run in delay mode (press d to toggle on/off) when you here a beep it will stop show arrows and attempt to use the blue direction angle (perpendicular to the line segment it's hitting) instead of the normal white reflective angle. (In delay mode, it will stop and show color coded arrows at every hit with boundary.)
When delay mode is not toggled, you will hear a BEEP and the beep will be counted but the circle just keeps moving the color coded arrows don't show up at that speed.
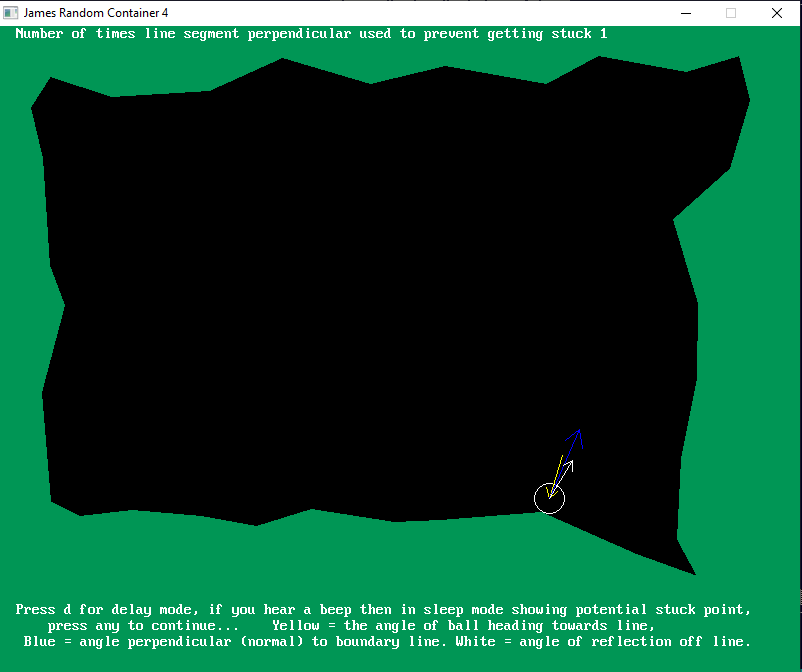
The circle does not get stuck at this peninsula, you don't see the white arrow pushing into the corner.
Here is a common example of when a circle does get stuck because the white arrow is headed straight into the point of peninsula and the lower body is going to collide with it. Here you can see why the blue arrow direction is the way out of being stuck.
Containing a bouncing circle inside a raggedy frame of random line segments, the problem arises, for me, of overcoming "stuck" points where the circle runs into a segment corner (called peninsulas by me) here the circle center may be clear of corner but it's lower body gets stuck pressing into corner.
First how to detect stick points in code?
2nd how to escape them?
To detect a stick, I just check the new coordinates of circle x, y if neither of them has changed, it's stuck.
If I find that condition then I change the ball angle to the perpendicular of the line segment (blue color code) it's mostly stuck at instead of using it's natural reflective angle (white color code). This seems to get the ball clear most every time.
There are times when ball gets wedged into a "bay" and this method of getting unstuck doesn't look like it would help much, the white arrow looks like the best way out but using the perpendicular doesn't seem to get it stuck worse...
See for yourself, let this demo run in delay mode (press d to toggle on/off) when you here a beep it will stop show arrows and attempt to use the blue direction angle (perpendicular to the line segment it's hitting) instead of the normal white reflective angle. (In delay mode, it will stop and show color coded arrows at every hit with boundary.)
When delay mode is not toggled, you will hear a BEEP and the beep will be counted but the circle just keeps moving the color coded arrows don't show up at that speed.
Code: (Select All)
Option _Explicit
_Title "James Random Container 4" ' b+ 2022-10-19
' Modify the lineSegIntersectCircle function to count number of points intersecting
' if more than one line segment do the one with the most points Yes! works better.
' Still can get a point stuck but it doesn't fly out of bounds.
' 2022-10-19 Aha! a simple solution to being stuck on peninsulas, just back out 1 more time
' nope, nor 2 more, nor until both x or y change more than a pixel
' Now we are getting stuck in bays as well as peninsulas! and it seems bad choice to use segment
' normal to get out of a bay, usually just follow white arrow for bays...
' Move Container making code into a sub and make doubly raggety changing min 80 to min 40
' Added delaid mode toggle with d keypresses listen for BEEP in this mode it goes into sleep mode.
' Have to press a key to continue...
Screen _NewImage(800, 680, 32)
_ScreenMove 250, 50
Randomize Timer
_PrintMode _KeepBackground
Type lineSegment
As Single x1, y1, x2, y2, dN ' 2 end points and an angle pointing towards center (I think)
End Type
Dim Shared As Long Container, Nlines, L
ReDim Shared Boundaries(1 To 100) As lineSegment
MakeContainer ' for background ball boundaries
Dim bx, by, ba, br, bspeed, diff, test, saveL, hits ' now for bouncing circles around
Dim saveBx, saveBy, Beeps, delaid ' more variables to handle getting stuck
bx = _Width / 2: by = _Height / 2: bspeed = 5
br = 15 ' make ball radius (br) at least 2* speed
ba = Rnd * 360 ' setup up ball in middle of screen/container random heading = ba (ball angle)
' ok just bounce ball around the polygon container
Do
_PutImage , Container, 0
Locate 1, 1: Print " Number of times line segment perpendicular used to prevent getting stuck"; Beeps
Circle (bx, by), br ' draw ball then calc next loaction
bx = bx + bspeed * CosD(ba) ' test x, y is new ball position if dont run into wall
by = by + bspeed * SinD(ba)
hits = 0: saveL = 0
For L = 1 To Nlines ' get line segment with highest hit count if any
test = lineSegIntersectCircle(Boundaries(L).x1, Boundaries(L).y1, Boundaries(L).x2, Boundaries(L).y2, bx, by, br)
If test > hits Then saveL = L: hits = test
Next
' probably should back it up before processing bounce
If hits Then ' backup circle
While lineSegIntersectCircle(Boundaries(saveL).x1, Boundaries(saveL).y1, Boundaries(saveL).x2, Boundaries(saveL).y2, bx, by, br) ' back up circle
bx = bx + CosD(ba - 180)
by = by + SinD(ba - 180)
Wend
'' getting over the peninsula's mod 2022-10-19 one more backout? this did not help much
'For i = 1 To 2
'bx = bx + CosD(ba - 180)
'by = by + SinD(ba - 180)
'Next
' =========================== fix penisula stick problem ???????????????????????????????????????????
_PutImage , Container, 0 ' show circle hit on boundary
Locate 1, 1: Print " Number of times line segment perpendicular used to prevent getting stuck"; Beeps
Circle (bx, by), br
' Yellow arrow for incoming towards boundary (I reversed the head of arrow to compare to reflection angle)
ArrowTo bx + 3 * br * CosD(ba + 180), by + 3 * br * SinD(ba + 180), ba, 3 * br, &HFFFFFF00
' Blue Vector Perpendicular to plane
ArrowTo bx, by, Boundaries(saveL).dN, 5 * br, &HFF0000FF
' Reflected ball off line are we stuck???
If Abs(bx - saveBx) > 1 Or Abs(by - saveBy) > 1 Then ' NO ball is moving right along
diff = Boundaries(saveL).dN - ba + 180
ba = Boundaries(saveL).dN + diff ' >>>> new direction
Else '>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> Quite likely stuck so use the normal angle for ba
If delaid Then
' show what I would normally do with ball
diff = Boundaries(saveL).dN - ba + 180
ba = Boundaries(saveL).dN + diff ' >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> new direction
ArrowTo bx, by, ba, 3 * br, &HFFFFFFFF
_Display
End If
Beep ' indicate by sound that the alternate angle for ball was used
Beeps = Beeps + 1
If delaid Then Sleep
' now fix angle to normal instead of regular method
ba = Boundaries(saveL).dN ' >>>>>>>>>>>>>>>>>>>>>>> new direction from line segment perpendicular angle
End If
ArrowTo bx, by, ba, 3 * br, &HFFFFFFFF
saveBx = bx: saveBy = by
_Display
If delaid Then _Delay 1 'comment out to find stucks faster
End If
If InKey$ = "d" Then delaid = 1 - delaid ' toggle dlaid mode
_Display
_Limit 300
Loop Until _KeyDown(27)
Sub MakeContainer
Dim cx, cy, x1, y1, flag, x2, y2 ' building container
Dim As _Unsigned Long c1
cx = _Width / 2: cy = _Height / 2 + 40
c1 = _RGB32(0, 150, 85) ' minty green background out of bounds
Cls
x1 = 50
y1 = 50
flag = 0
While flag = 0
x2 = (Rnd * 80) + 40 + x1
If x2 > 750 Then
x2 = 750
flag = 1
End If
y2 = Rnd * 60 + 20
Line (x1, y1)-(x2, y2), c1
Nlines = Nlines + 1
Boundaries(Nlines).x1 = x1: Boundaries(Nlines).y1 = y1
Boundaries(Nlines).x2 = x2: Boundaries(Nlines).y2 = y2
Boundaries(Nlines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
flag = 0
While flag = 0
y2 = (Rnd * 80) + 40 + y1
If y2 > 550 Then
y2 = 550
flag = 1
End If
x2 = 750 - (Rnd * 60 + 20)
Line (x1, y1)-(x2, y2), c1
Nlines = Nlines + 1
Boundaries(Nlines).x1 = x1: Boundaries(Nlines).y1 = y1
Boundaries(Nlines).x2 = x2: Boundaries(Nlines).y2 = y2
Boundaries(Nlines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
flag = 0
While flag = 0
x2 = x1 - ((Rnd * 80) + 40)
If x2 < 50 Then
x2 = 50
flag = 1
End If
y2 = 550 - (Rnd * 60 + 20)
Line (x1, y1)-(x2, y2), c1
Nlines = Nlines + 1
Boundaries(Nlines).x1 = x1: Boundaries(Nlines).y1 = y1
Boundaries(Nlines).x2 = x2: Boundaries(Nlines).y2 = y2
Boundaries(Nlines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
flag = 0
While flag = 0
y2 = y1 - ((Rnd * 80) + 40)
If y2 < 50 Then
y2 = 50
flag = 1
End If
x2 = Rnd * 60 + 20
If flag = 1 Then x2 = 50
Line (x1, y1)-(x2, y2), c1
Nlines = Nlines + 1
Boundaries(Nlines).x1 = x1: Boundaries(Nlines).y1 = y1
Boundaries(Nlines).x2 = x2: Boundaries(Nlines).y2 = y2
Boundaries(Nlines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
Paint (1, 1), c1, c1
Locate 37, 1
Print " Press d for delay mode, if you hear a beep then in sleep mode showing potential stuck point,"
Print " press any to continue... Yellow = the angle of ball heading towards line,"
Print " Blue = angle perpendicular (normal) to boundary line. White = angle of reflection off line."
Container = _NewImage(_Width, _Height, 32)
_PutImage , 0, Container
End Sub
' return count of how many points overlap segment
Function lineSegIntersectCircle (x1, y1, x2, y2, cx, cy, r)
' x1, y1 and x2, y2 are end points of line segment
' cx, cy are circle center with radius r
Dim rtn, d, dx, dy, i, x, y
d = Sqr((x1 - x2) ^ 2 + (y1 - y2) ^ 2)
dx = (x2 - x1) / d
dy = (y2 - y1) / d
For i = 0 To d
x = x1 + dx * i
y = y1 + dy * i
If Sqr((x - cx) ^ 2 + (y - cy) ^ 2) <= r Then rtn = rtn + 1
Next
lineSegIntersectCircle = rtn
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
CosD = Cos(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
SinD = Sin(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2) makes to a first point (x1, y1)
' Note this function uses whatever the default type is, better not be some Integer Type.
' Delta means change between 1 measure and another for example x2 - x1
Dim deltaX, deltaY, rtn
deltaX = x2 - x1
deltaY = y2 - y1
' To find the angle point(x2, y2) makes to (x1, y1) in Degrees
' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
rtn = _R2D(_Atan2(deltaY, deltaX))
If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function
' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
Dim As Long x1, y1, x2, y2, x3, y3
Dim As Double rAngle
rAngle = _D2R(dAngle)
x1 = BaseX + lngth * Cos(rAngle)
y1 = BaseY + lngth * Sin(rAngle)
x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
Line (BaseX, BaseY)-(x1, y1), colr
Line (x1, y1)-(x2, y2), colr
Line (x1, y1)-(x3, y3), colr
End SubThe circle does not get stuck at this peninsula, you don't see the white arrow pushing into the corner.
Here is a common example of when a circle does get stuck because the white arrow is headed straight into the point of peninsula and the lower body is going to collide with it. Here you can see why the blue arrow direction is the way out of being stuck.
b = b + ...