Posts: 1,507
Threads: 160
Joined: Apr 2022
Reputation:
116
Here's something I noticed the other day, which I thought might interest you, since you've written a ton of programs regarding prime numbers -- most primes tend to be multiples of 6, +/- 1!
5 is 6 -1
7 is 6 + 1
11 is 6 * 2 -1
13 is 6 * 2 +1
17 is 6 * 3 -1
19 is 6 x 3 +1
... and so on.
I don't know how far the pattern continues (past 100, I think), but you might want to play with it some and see how it holds up in general. It may be a quicker way to generate a list of primes than using the Sieve which I've seen you implement often in the past. My ass is still kicked from my last doctor's visit and all, and I'm not up to coding on it at the moment, but I figured I'd share the observation in case it interested you. 
Posts: 2,700
Threads: 124
Joined: Apr 2022
Reputation:
134
(06-30-2022, 10:49 AM)SMcNeill Wrote: Here's something I noticed the other day, which I thought might interest you, since you've written a ton of programs regarding prime numbers -- most primes tend to be multiples of 6, +/- 1!
5 is 6 -1
7 is 6 + 1
11 is 6 * 2 -1
13 is 6 * 2 +1
17 is 6 * 3 -1
19 is 6 x 3 +1
... and so on.
I don't know how far the pattern continues (past 100, I think), but you might want to play with it some and see how it holds up in general. It may be a quicker way to generate a list of primes than using the Sieve which I've seen you implement often in the past. My ass is still kicked from my last doctor's visit and all, and I'm not up to coding on it at the moment, but I figured I'd share the observation in case it interested you. 
Yes it is a small 6 wheel: 2*3, next one up is 30 wheel: 2*3*5, and next one up is 210 wheel: 2*3*5*7
Wheels speed up Prime Sieving because there is no IF checking and much fewer loops. Smallest wheel is 2: odd and even numbers. Euclid: Primes are Infinite because Wheel + 1 is not divisible to all previous known primes (but not necessarily prime though very often is).
b = b + ...
Posts: 2,700
Threads: 124
Joined: Apr 2022
Reputation:
134
06-30-2022, 12:29 PM
(This post was last modified: 06-30-2022, 12:30 PM by bplus.)
Here is Prime Sieving with a 6 wheeler:
Code: (Select All) ' 6 wheel sieve.bas for QB64 fork (B+=MGA) 2017-08-30 copy and trans to QB64
'translated from: First Factors.bas for SmallBASIC 11/27/14 (bpf.org post)
'topN = 1000000, primes 78,498, .17 secs, 8169 twins last 999959, 999961
'topN = 10000000, primes 664,579, 1.85 secs, 58,980 twins last 9999971, 9999973
'topN = 100000000, primes 5,761,455, 20.69 secs, 440,312 twins last 99999587, 99999589
' out of memory for 1 billion
'compare to 30 wheel
'topN = 1000000, primes 78,498, .15 secs, 8169 twins last 999959, 999961
'topN = 10000000, primes 664,579, 1.81 secs, 58,980 twins last 9999971, 9999973
'topN = 100000000, primes 5,761,455, 19.65 secs, 440,312 twins last 99999587, 99999589
' out of memory for 1 billion
'compare to 2310 wheel sieve WOW the 30 wheel is faster!
'QB64 results from 2310 wheel
'topN = 1000000, primes 78,498, .18 secs, 8169 twins last 999959, 999961
'topN = 10000000, primes 664,579, 1.98 secs, 58,980 twins last 9999971, 9999973
'topN = 100000000, primes 5,761,455, 21.57 secs, 440,312 twins last 99999587, 99999589
' out of memory for 1 billion
_Define A-Z As _INTEGER64
Option Base 1
Common Shared ff(), topN
topN = 1223 'first 200 primes test
topN = 100000000
testlimitN = Sqr(topN)
'First Factors array is 0 for prime number or contains the numbers lowest factor
Dim ff(topN + 6)
tStart# = Timer(.001)
For i = 0 To topN Step 6
ff(i + 2) = 2: ff(i + 3) = 3: ff(i + 4) = 2: ff(i + 6) = 2
Next
ff(2) = 0: ff(3) = 0 'fix first 2 factors
For pcand = 5 To testlimitN Step 2
If ff(pcand) = 0 Then
For i = pcand * pcand To topN Step 2 * pcand
If ff(i) = 0 Then ff(i) = pcand
Next
End If
Next
'count primes
For i = 2 To topN
If ff(i) = 0 Then p = p + 1
Next
tStop# = Timer(.001)
tTime# = tStop# - tStart#
Print "For "; topN; " numbers there are "; p; " primes in "; tTime#; " secs."
If 0 Then ' <<<<< uncomment this as needed
'file twin primes data
Open "Twin primes.txt" For Output As #1
lastp = -1
For i = 2 To topN
If ff(i) = 0 Then
If i - lastp = 2 Then
Print #1, Str$(lastp) + ", " + Str$(i) + " Middle/6 = " + Str$((i - 1) / 6) + ": " + factors$((i - 1) / 6)
tCount = tCount + 1
End If
lastp = i
End If
Next
Close #1
Print "Found "; tCount; " Twin Primes in first "; topN; " integers."
End If ' <<<<<<<<<<<<< uncomment this as needed
'test some factoring of numbers
factorMe = 10
While factorMe > 1
Input "Enter a number to factor, 0 quits "; factorMe
If factorMe < 2 Then Exit While Else Print factors$(factorMe)
Wend
Function factors$ (n)
If n > topN Then factors$ = "Error: too high a number.": Exit Function
f$ = ""
While ff(n) <> 0
f$ = f$ + Str$(ff(n)) + " "
n = n / ff(n)
Wend
factors$ = f$ + Str$(n)
End Function
PLUS: Once we have established primes, we can quickly factor numbers.
b = b + ...
Posts: 20
Threads: 2
Joined: Apr 2022
Reputation:
3
Here's one that I wrote for QB4.5 (amazingly you can go up to 100 million despite the memory restrictions).
Code: (Select All) Rem finding primes to 100 million!!!
TT = Timer
DefLng I-N
N = 3226000
Dim A(0 To N) As Long
Dim B(0 To 30) As Long
B(0) = 1
For I = 1 To 30
B(I) = B(I - 1) + B(I - 1)
Next I
For J = 2 To 5000
J1 = J \ 31: J2 = J Mod 31
If (A(J1) And B(J2)) = 0 Then
K1 = J + J - 1
K2 = K1 * J - K1 + J
For I = K2 To 50000000 Step K1
I1 = I \ 31: I2 = I Mod 31
A(I1) = (A(I1) Or B(I2))
Next I
End If
Next J
Rem *** End of main routine - Printout starts here ***
'PRINT " 2 ";
For I = 2 To 50000000
I1 = I \ 31: I2 = I Mod 31
L = A(I1) And B(I2)
If L = 0 Then
'PRINT I + I - 1; 'unrem to print
L1 = L1 + 1
End If
Next I
Print "Number of primes to 100M = "; L1 + 1; Timer - TT
Posts: 2,700
Threads: 124
Joined: Apr 2022
Reputation:
134
(06-30-2022, 12:46 PM)david_uwi Wrote: Here's one that I wrote for QB4.5 (amazingly you can go up to 100 million despite the memory restrictions).
Code: (Select All) Rem finding primes to 100 million!!!
TT = Timer
DefLng I-N
N = 3226000
Dim A(0 To N) As Long
Dim B(0 To 30) As Long
B(0) = 1
For I = 1 To 30
B(I) = B(I - 1) + B(I - 1)
Next I
For J = 2 To 5000
J1 = J \ 31: J2 = J Mod 31
If (A(J1) And B(J2)) = 0 Then
K1 = J + J - 1
K2 = K1 * J - K1 + J
For I = K2 To 50000000 Step K1
I1 = I \ 31: I2 = I Mod 31
A(I1) = (A(I1) Or B(I2))
Next I
End If
Next J
Rem *** End of main routine - Printout starts here ***
'PRINT " 2 ";
For I = 2 To 50000000
I1 = I \ 31: I2 = I Mod 31
L = A(I1) And B(I2)
If L = 0 Then
'PRINT I + I - 1; 'unrem to print
L1 = L1 + 1
End If
Next I
Print "Number of primes to 100M = "; L1 + 1; Timer - TT
That's pretty fast @david_uwi, looks like a variation on a 30 wheeler, 1.5 secs on my system, mine takes 2.5 plus but mine can factor numbers once the sieving is complete. Shall we have a look at my 2310 wheeler? ought to do much better now that I am using 0.8.2 with optimized compiler. ;-))
b = b + ...
Posts: 20
Threads: 2
Joined: Apr 2022
Reputation:
3
Of course that wouldn't work in qb4.5 (I have redimensioned the arrays) in qb4.5 you can only get to 2 million (array limitations) or use the hard disc as storage which is very slow.
There is nothing clever in the program it just uses "the sieve" and stores the primes in a binary array for use in finding the next prime...
Posts: 40
Threads: 2
Joined: May 2022
07-01-2022, 11:29 AM
(This post was last modified: 07-01-2022, 11:31 AM by triggered.)
This brutal program looks at a different issue but reminds me of what's going on here. It turns out that every odd number can be produced by a formula
a = (x * 2^y - 1) / 3
... for some pair x, y (as long as x is indivisible by 3). This particular relation is used to help say things about the Collatz conjecture if anyone wants to reverse engineer it. For some reason, this code runs slower in later versions of QB64, faster in the SDL version, and fastest in QBjs. Not even close to ready when tried in the BAM.
Code: (Select All) 'DefInt A-Z
Dim i, x, y, a, f, xlim, ylim
xlim = 1500
ylim = 1500
For i = 1 To 1001 Step 2
f = 0
x = 0
Do While (f = 0) And (x < xlim)
y = 0
If (x Mod 3) <> 0 Then
Do While (f = 0) And (y < ylim)
a = (x * (2 ^ y) - 1) / 3
If (a = i) Then
Print a; "= ("; _Trim$(Str$(x)); " * 2^"; _Trim$(Str$(y)); ") - 1) / 3"
f = 1
End If
If (f = 1) Then Exit Do
y = y + 1
Loop
If (f = 1) Then Exit Do
End If
x = x + 1
Loop
If (f = 0) Then
Print i; "Increase xlim or ylim."
Beep
End If
Next
Posts: 1,507
Threads: 160
Joined: Apr 2022
Reputation:
116
I sat and wrote one of these this morning, just to pass the time:
Code: (Select All) $Checking:Off
DefLng A-Z: Const Limit = 10000000: Dim Shared primes(10000000)
primes(1) = 2: primes(2) = 3: n = 2 'preload the first two primes.
t# = Timer
num = -1
Do
num = num + 6
If CheckPrime(num) Then n = n + 1: primes(n) = num
If CheckPrime(num + 2) Then n = n + 1: primes(n) = num + 2
Loop Until num >= Limit
Print Using "###.### seconds to generate ###,###,###,### primes"; Timer - t#, n
Function CheckPrime (num)
s = Sqr(num)
For i = 1 To 10000000
If primes(i) > s Then Exit For Else If num Mod primes(i) = 0 Then Exit Function
Next
CheckPrime = -1
End Function
Seems a little shorter and simpler than what you guys have posted, but the time runs almost *exactly* the same on my machine as the times which bplus has posted in his examples above -- with the exception being the final 100,000,000 test. For some reason, the times for it seems to be about twice the time as what bplus has listed. Are you certain that 20 second time is correct? If so, then why the heck does this hold so perfectly relatable to the other times, and then suddenly jump off course with the final test??
Anywho, I'll play around with this a bit more later and see if I can't come up with a method which might be faster than this. It's always fun to try and optimize something for speed and performance. 
Posts: 2,700
Threads: 124
Joined: Apr 2022
Reputation:
134
Quote:Are you certain that 20 second time is correct?
For first 100,000,000 integers the 6 wheeler takes 2.5+ secs as posted in reply #6 to david_uwi in current QB64 v0.8.2 with compiler optimized. David's takes even less time, 1.5 secs on my system, but I don't think he is saving first factor information like I am to actually use the prime/composite array for something practical like factoring numbers.
The 20 secs time was back in 2017 probably on my old dinosaur laptop and old version of QB64.
If you are using the test: if pc mod p = 0 then pc is prime (prime candidate mod prime = 0 ie p divides pc), that is very slow test.
b = b + ...
Posts: 2,700
Threads: 124
Joined: Apr 2022
Reputation:
134
I just ran all 3 on my system and David's is winner (Windows 10 laptop, QB64 v 0.8.2 with compiler optimized)
Steve, yours ran for 20+ secs by far the slowest time:
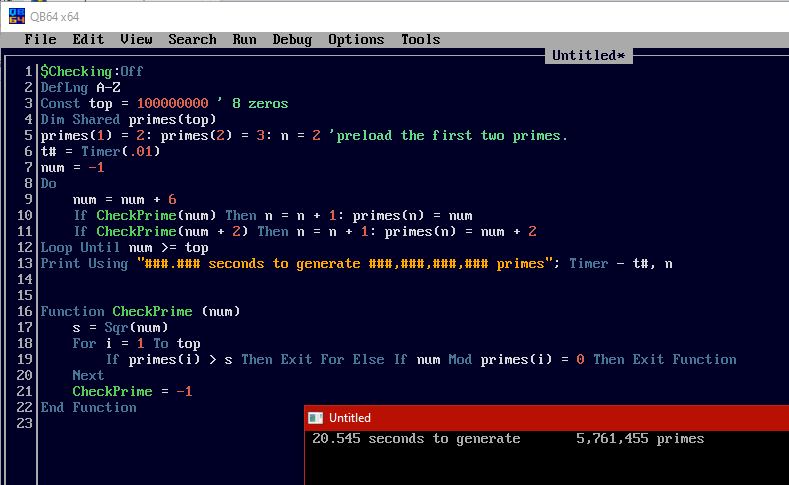
Mine fell in middle 2.6+ secs this time:
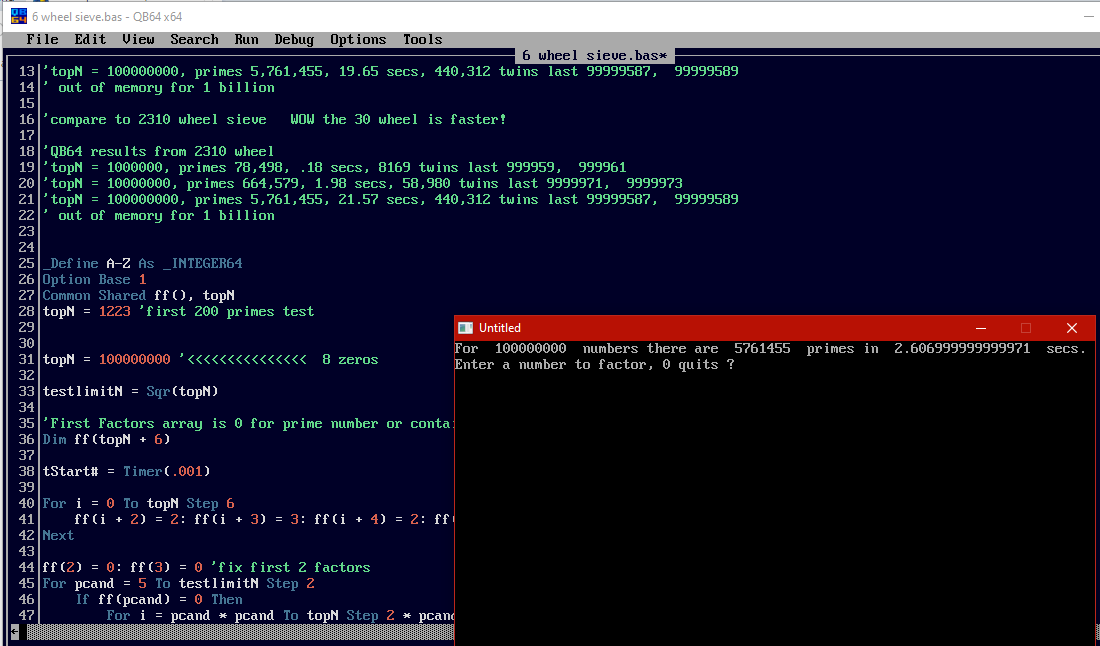
David's clear winner in speed contest of counting only:
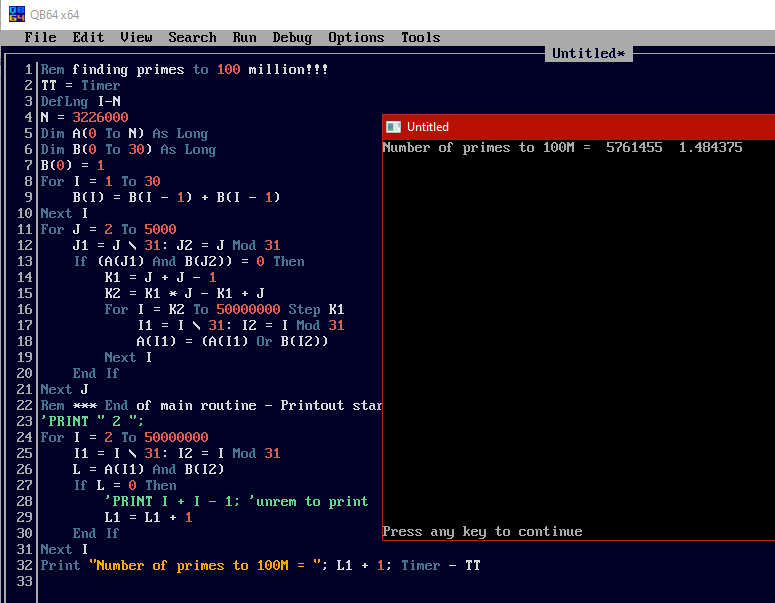
b = b + ...
|





