10-17-2022, 10:07 AM
(This post was last modified: 10-17-2022, 10:37 AM by bplus.
Edit Reason: Get rid of unused variables in DIM, resize screen, lose last print line
)
Aha! I got it, no vectors needed!
I had to create a new Function for detecting a line segment inside a circle. This is that:
OK best to just think of a circle as a distance from a given point and basically redraw the line point by point and see that each point is in range of circle radius.
Here is James Container #2 with his code for creating the container for the circle to bounce inside (changed border color):
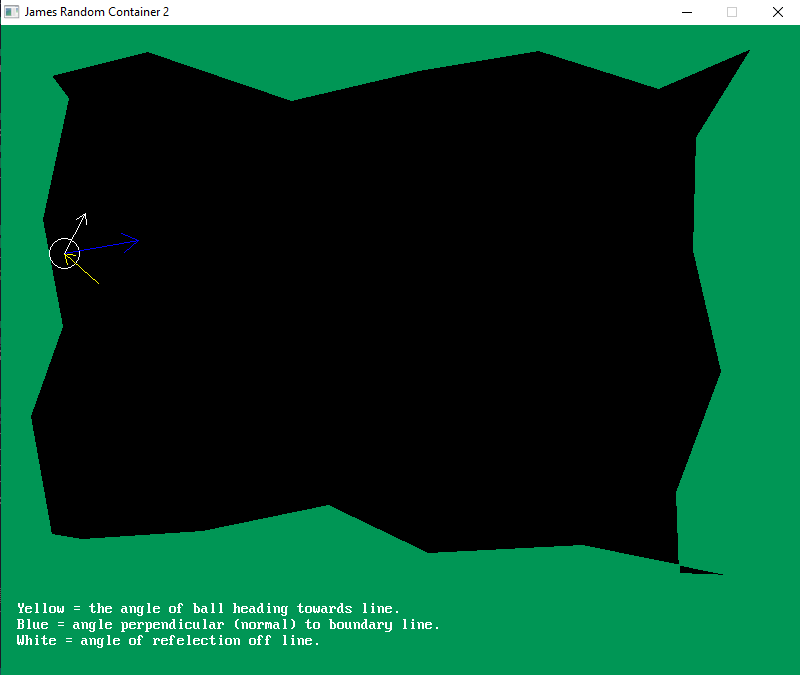
The circle will occasionally jump out of the boundary and fly off. I think it is picking the wrong line to bounce off of as a couple line segments could be in range of the circle when checked. I also had to keep speed (in pixels) well below the pixel radius or the circle will be "returned" to the wrong side of the line on the outside of boundary line.
I might be able to reduce the occasional fly off, just got an idea....
Update: When it flies off it is not following the direction of the white arrow for some reason, not because it is picking the wrong line segment .
I had to create a new Function for detecting a line segment inside a circle. This is that:
Code: (Select All)
' return 0 if no overlap
Function lineSegIntersectCircle% (x1, y1, x2, y2, cx, cy, r)
' x1, y1 and x2, y2 are end points of line segment
' cx, cy are circle center with radius r
Dim d, dx, dy, i, x, y
d = Sqr((x1 - x2) ^ 2 + (y1 - y2) ^ 2)
dx = (x2 - x1) / d
dy = (y2 - y1) / d
For i = 0 To d
x = x1 + dx * i
y = y1 + dy * i
If Sqr((x - cx) ^ 2 + (y - cy) ^ 2) <= r Then lineSegIntersectCircle% = -1: Exit Function
Next
End FunctionOK best to just think of a circle as a distance from a given point and basically redraw the line point by point and see that each point is in range of circle radius.
Here is James Container #2 with his code for creating the container for the circle to bounce inside (changed border color):
Code: (Select All)
Option _Explicit
_Title "James Random Container 2" ' b+ 2022-10-16
Screen _NewImage(800, 680, 32)
_ScreenMove 250, 50
Randomize Timer
_PrintMode _KeepBackground
Type lineSegment
As Single x1, y1, x2, y2, dN ' 2 end points
End Type
' mod RegularPoly to save lines created by
Dim cx, cy, x1, y1, flag, x2, y2 ' building container
Dim As _Unsigned Long c1
Dim As Long NLines, L, Container
ReDim Boundaries(1 To 100) As lineSegment
cx = _Width / 2: cy = _Height / 2 + 40
c1 = _RGB32(0, 150, 85) ' minty green background out of bounds
Cls
x1 = 50
y1 = 50
flag = 0
While flag = 0
x2 = (Rnd * 80) + 80 + x1
If x2 > 750 Then
x2 = 750
flag = 1
End If
y2 = Rnd * 60 + 20
Line (x1, y1)-(x2, y2), c1
NLines = NLines + 1
Boundaries(NLines).x1 = x1: Boundaries(NLines).y1 = y1
Boundaries(NLines).x2 = x2: Boundaries(NLines).y2 = y2
Boundaries(NLines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
flag = 0
While flag = 0
y2 = (Rnd * 80) + 80 + y1
If y2 > 550 Then
y2 = 550
flag = 1
End If
x2 = 750 - (Rnd * 60 + 20)
Line (x1, y1)-(x2, y2), c1
NLines = NLines + 1
Boundaries(NLines).x1 = x1: Boundaries(NLines).y1 = y1
Boundaries(NLines).x2 = x2: Boundaries(NLines).y2 = y2
Boundaries(NLines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
flag = 0
While flag = 0
x2 = x1 - ((Rnd * 80) + 80)
If x2 < 50 Then
x2 = 50
flag = 1
End If
y2 = 550 - (Rnd * 60 + 20)
Line (x1, y1)-(x2, y2), c1
NLines = NLines + 1
Boundaries(NLines).x1 = x1: Boundaries(NLines).y1 = y1
Boundaries(NLines).x2 = x2: Boundaries(NLines).y2 = y2
Boundaries(NLines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
flag = 0
While flag = 0
y2 = y1 - ((Rnd * 80) + 80)
If y2 < 50 Then
y2 = 50
flag = 1
End If
x2 = Rnd * 60 + 20
If flag = 1 Then x2 = 50
Line (x1, y1)-(x2, y2), c1
NLines = NLines + 1
Boundaries(NLines).x1 = x1: Boundaries(NLines).y1 = y1
Boundaries(NLines).x2 = x2: Boundaries(NLines).y2 = y2
Boundaries(NLines).dN = DAtan2(x1, y1, x2, y2) + 90 ' the angle x2, y2 is to x1, y1 + 90 points inward
x1 = x2
y1 = y2
Wend
Paint (1, 1), c1, c1
Locate 37, 1
Print " Yellow = the angle of ball heading towards line."
Print " Blue = angle perpendicular (normal) to boundary line."
Print " White = angle of refelection off line."
Container = _NewImage(_Width, _Height, 32)
_PutImage , 0, Container
Dim bx, by, ba, br, bspeed, diff
bx = cx: by = cy: bspeed = 5
br = 15 ' make ball radius (br) at least 2* speed
ba = Rnd * 360 ' setup up ball in middle of screen/container random heading = ba (ball angle)
' ok just bounce ball around the polygon container
Do
_PutImage , Container, 0
Circle (bx, by), br ' draw ball then calc next loaction
bx = bx + bspeed * CosD(ba) ' test x, y is new ball position if dont run into wall
by = by + bspeed * SinD(ba)
For L = 1 To NLines ' did we hit any?
' probably should back it up before processing bounce
If lineSegIntersectCircle%(Boundaries(L).x1, Boundaries(L).y1, Boundaries(L).x2, Boundaries(L).y2, bx, by, br) Then ' rebound ball
Sound 1000, .5
While lineSegIntersectCircle%(Boundaries(L).x1, Boundaries(L).y1, Boundaries(L).x2, Boundaries(L).y2, bx, by, br) ' back up circle
bx = bx + CosD(ba - 180)
by = by + SinD(ba - 180)
Wend
_PutImage , Container, 0 ' show circle hit on boundary
Circle (bx, by), br
' Yellow arrow for incoming towards boundary (I reversed the head of arrow to compare to reflection angle)
ArrowTo bx + 3 * br * CosD(ba + 180), by + 3 * br * SinD(ba + 180), ba, 3 * br, &HFFFFFF00
' Blue Vector Perpendicular to plane
ArrowTo bx, by, Boundaries(L).dN, 5 * br, &HFF0000FF
' Reflected ball off line
diff = Boundaries(L).dN - ba + 180
ba = Boundaries(L).dN + diff ' >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> new direction
ArrowTo bx, by, ba, 3 * br, &HFFFFFFFF
_Display
_Delay 2
End If
Next
_Display
_Limit 120
Loop Until _KeyDown(27)
' return 0 if no overlap
Function lineSegIntersectCircle% (x1, y1, x2, y2, cx, cy, r)
' x1, y1 and x2, y2 are end points of line segment
' cx, cy are circle center with radius r
Dim d, dx, dy, i, x, y
d = Sqr((x1 - x2) ^ 2 + (y1 - y2) ^ 2)
dx = (x2 - x1) / d
dy = (y2 - y1) / d
For i = 0 To d
x = x1 + dx * i
y = y1 + dy * i
If Sqr((x - cx) ^ 2 + (y - cy) ^ 2) <= r Then lineSegIntersectCircle% = -1: Exit Function
Next
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
CosD = Cos(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
SinD = Sin(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2) makes to a first point (x1, y1)
' Note this function uses whatever the default type is, better not be some Integer Type.
' Delta means change between 1 measure and another for example x2 - x1
Dim deltaX, deltaY, rtn
deltaX = x2 - x1
deltaY = y2 - y1
' To find the angle point(x2, y2) makes to (x1, y1) in Degrees
' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
rtn = _R2D(_Atan2(deltaY, deltaX))
If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function
' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
Dim As Long x1, y1, x2, y2, x3, y3
Dim As Double rAngle
rAngle = _D2R(dAngle)
x1 = BaseX + lngth * Cos(rAngle)
y1 = BaseY + lngth * Sin(rAngle)
x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
Line (BaseX, BaseY)-(x1, y1), colr
Line (x1, y1)-(x2, y2), colr
Line (x1, y1)-(x3, y3), colr
End SubThe circle will occasionally jump out of the boundary and fly off. I think it is picking the wrong line to bounce off of as a couple line segments could be in range of the circle when checked. I also had to keep speed (in pixels) well below the pixel radius or the circle will be "returned" to the wrong side of the line on the outside of boundary line.
I might be able to reduce the occasional fly off, just got an idea....
Update: When it flies off it is not following the direction of the white arrow for some reason, not because it is picking the wrong line segment .
b = b + ...



