05-10-2022, 08:22 PM
OK to get closer to drawing with a Spirograph, we need to play around within inner gear sizes.
BTW do we need toothed gears? Heck no! Toothed Gears are for people with real Spirographs so circle doesn't slide around. Gears are allot of extra trouble and even Walter's, a very professional looking Spirograph, has the teeth misaligned! (Yeah look closer!)
So in Test 2 we change sizes of inner radius as ratio's to outer radius 1/2, 1/3, 1/4, ...
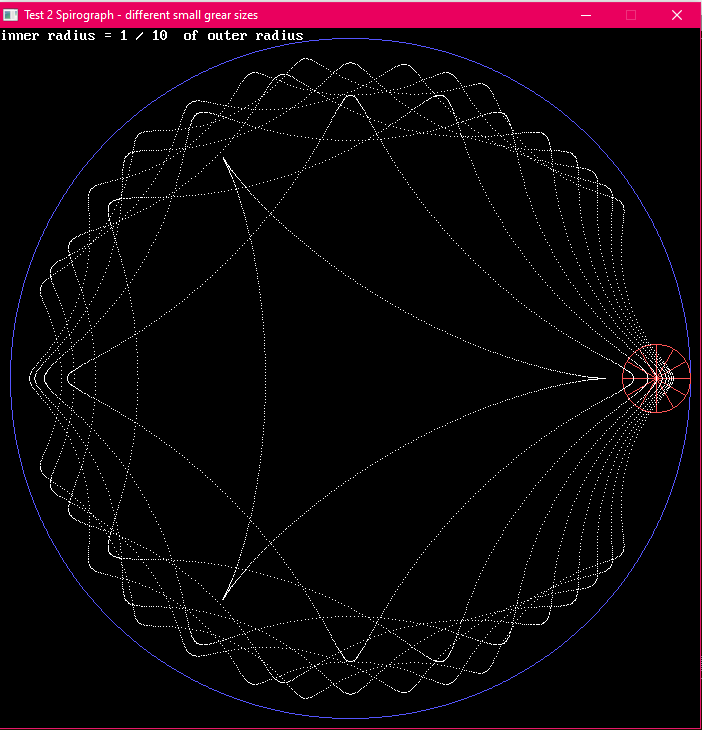
Looks right to me ;-)) as the ratio increases by 1 the number of sides drawn increases by 1. This draws a perfectly enclosed figure each round because the smaller radius divides the larger perfectly.
BTW do we need toothed gears? Heck no! Toothed Gears are for people with real Spirographs so circle doesn't slide around. Gears are allot of extra trouble and even Walter's, a very professional looking Spirograph, has the teeth misaligned! (Yeah look closer!)
So in Test 2 we change sizes of inner radius as ratio's to outer radius 1/2, 1/3, 1/4, ...
Code: (Select All)
_Title "Test 2 Spirograph - different small gear sizes" 'b+ 2022-05-10 trans from
'Spirograph RO divided by 2 - 10 = RI.bas SmallBASIC 0.12.9 (B+=MGA) 2017-07-01
xmax = 700: ymax = 700
Screen _NewImage(xmax, ymax, 12) ' using 16 colors
_ScreenMove 300, 20
Dim Shared pi
pi = _Pi
Dim Shared px(20000), py(20000), pIndex
rO = ymax / 2 - 10 ' fit screen radius of big circle
Ox = xmax / 2
Oy = ymax / 2
pIndex = 0
For ir = 2 To 10
rI = rO / ir ' smaller circle that travels inside edge of larger
OI = rO / rI ' rate inner circle spins compared to angle on outer circle
For a = 0 To 2 * pi Step pi / 360 'while the inner circle contacts outer at angle a
Cls
Color 15
Print "inner radius = 1 /"; ir; " of outer radius"
Circle (Ox, Oy), rO, 9
'the origin of inner circle at same angle
Ix = Ox + (rO - rI) * Cos(a)
Iy = Oy + (rO - rI) * Sin(a)
Ia = OI * a 'the angle of the inner points are OI * a on outer circle
'draw line from origin of inner circle to outer edge
Color 12
wheel Ix, Iy, rI, -Ia
For i = 0 To pIndex - 1
PSet (px(i), py(i)), 15
Next
_Display
_Delay .01
Next
Next
Sleep
Sub wheel (x, y, r, a)
'local i, x1, y1
Circle (x, y), r
For i = 1 To 12
x1 = x + r * Cos(i * 2 * pi / 12 + a)
y1 = y + r * Sin(i * 2 * pi / 12 + a)
Line (x, y)-(x1, y1)
If i = 12 Then
x2 = x + r / 2 * Cos(i * 2 * pi / 12 + a)
y2 = y + r / 2 * Sin(i * 2 * pi / 12 + a)
px(pIndex) = x2
py(pIndex) = y2
pIndex = pIndex + 1
End If
Next
End SubLooks right to me ;-)) as the ratio increases by 1 the number of sides drawn increases by 1. This draws a perfectly enclosed figure each round because the smaller radius divides the larger perfectly.
b = b + ...



