05-10-2022, 08:59 PM
And now let's go back and try what Ashish attempted at start, Wheel within wheel within..., only not 10 times!
Just a couple is enough, I think:
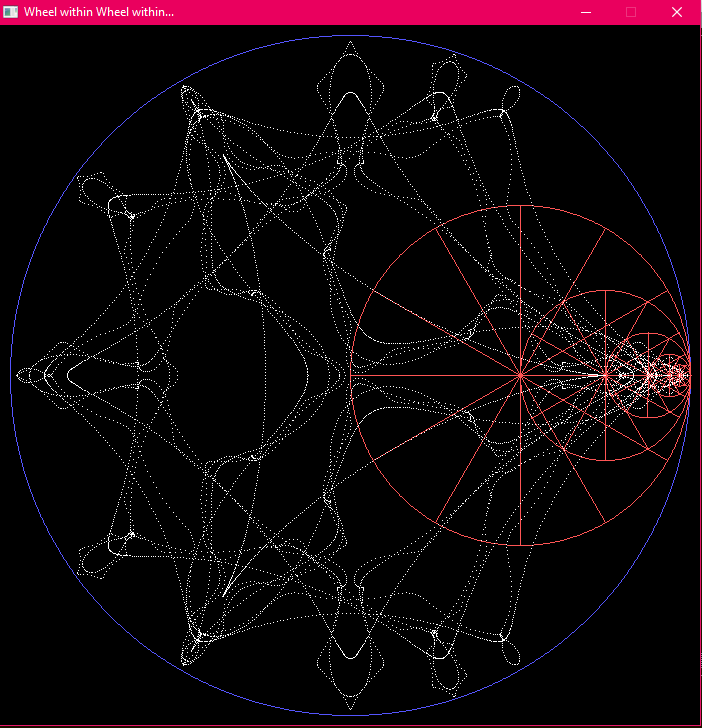
So there is proof of concept of gears within gears but!
A real physical Spirograph wouldn't work because you have to keep pressure on the gears to keep the teeth in the grooves, eventually that pressure will work against that goal when pushing one way will throw gears out on the opposite side you are pushing.
Just a couple is enough, I think:
Code: (Select All)
_Title "Wheel within Wheel within..." ' b+ 2022-05-10 from
'Spirograph wheels within wheels.bas SmallBASIC 0.12.9 (B+=MGA) 2017-07-02
xmax = 700: ymax = 700
Screen _NewImage(xmax, ymax, 12) ' using 16 colors
_ScreenMove 300, 20
Dim Shared pi
pi = _Pi
Dim Shared px(20000), py(20000), pIndex, ir
rO = ymax / 2 - 10 ' fit screen radius of big circle
Ox = xmax / 2
Oy = ymax / 2
pIndex = 0
Dim mark(4) ' mark the places of transition of pIndex's
m = 0: mark(0) = 0
For ir = 2 To 5 'Step -1
rI = rO / ir ' smaller circle that travels inside edge of larger
OI = rO / rI ' rate inner circle spins compared to angle on outer circle
For a = 0 To 2 * pi Step pi / 360 'while the inner circle contacts outer at angle a
Cls
Circle (Ox, Oy), rO, 9
'the origin of inner circle at same angle
Ix = Ox + (rO - rI) * Cos(a)
Iy = Oy + (rO - rI) * Sin(a)
Ia = OI * a 'the angle of the inner points are OI * a on outer circle
'draw line from origin of inner circle to outer edge
Color 12
wheel Ix, Iy, rI, -Ia
For i = 0 To pIndex - 1
PSet (px(i), py(i)), 15
Next
_Display
_Delay .01
Next
m = m + 1
mark(m) = pIndex - 1
Next
_Delay 2
For j = 0 To m - 1
Color 15: Cls
For i = mark(j) To mark(j + 1) - 1
PSet (px(i), py(i)), 15
Next
Print "Press any..."
_Display
Sleep
Next
Sub wheel (x, y, r, a)
'local i, x1, y1, x2, y2, rI2, Ix2, Iy2, Ia2
Circle (x, y), r
For i = 1 To 12
x1 = x + r * Cos(i * 2 * pi / 12 + a)
y1 = y + r * Sin(i * 2 * pi / 12 + a)
Line (x, y)-(x1, y1)
If i = 12 Then
x2 = x + r / 2 * Cos(i * 2 * pi / 12 + a)
y2 = y + r / 2 * Sin(i * 2 * pi / 12 + a)
px(pIndex) = x2
py(pIndex) = y2
pIndex = pIndex + 1
End If
Next
If r > 20 Then
rI2 = r / ir
Ix2 = x + (r - rI2) * Cos(a)
Iy2 = y + (r - rI2) * Sin(a)
Ia2 = r / rI2 * a
wheel Ix2, Iy2, rI2, -Ia2
End If
End SubSo there is proof of concept of gears within gears but!
A real physical Spirograph wouldn't work because you have to keep pressure on the gears to keep the teeth in the grooves, eventually that pressure will work against that goal when pushing one way will throw gears out on the opposite side you are pushing.
b = b + ...