Fractals

[bplus]

I liked that fractal so much I told a little story in code how it was born:

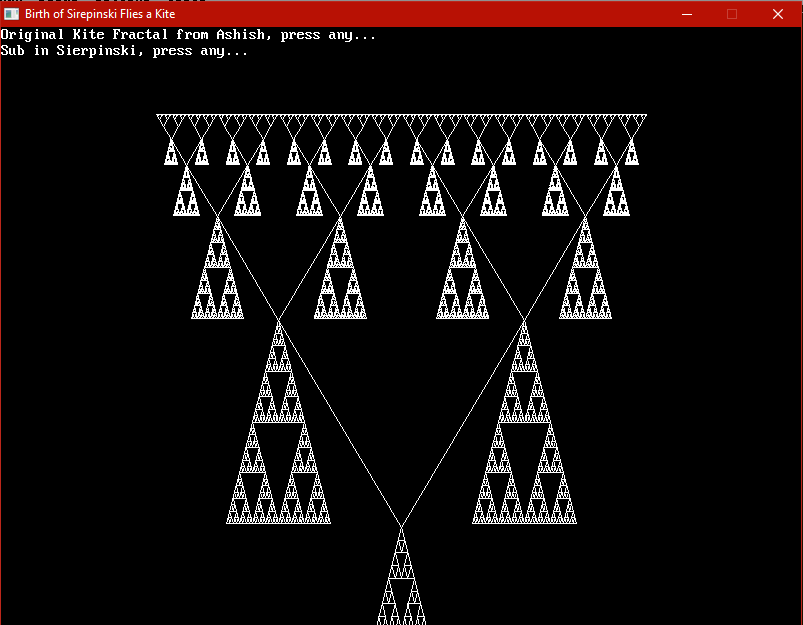
Birth of Sierpinski Flies a Kite

Code: (Select All)

_Title "Birth of Sirepinski Flies a Kite" 'b+ 2020-01-02
Screen _NewImage(800, 600, 32)
_ScreenMove 300, 50
drawKite 400, 500, 140, .5 'here was Ashish fractal, now put a 2 after drawKite
Print "Original Kite Fractal from Ashish, press any..."
Sleep
drawKite2 400, 500, 140, .5
Print "Sub in Sierpinski, press any..."
Sleep
Cls
drawKite2 400, 500, 140, -.5
Print "Mess with the a variable, press any..."
Sleep
For i = -1 To 1 Step .1
    Cls
    drawKite2 400, 500, 140, i
    Print "Run a continuous change on variable a, press any..."
    _Limit 15
Next
Sleep
For i = _Pi(-2) To _Pi(2) Step .1
    Cls
    drawKite2 400, 500, 140, i
    Print "Oh more continuous change on variable a, press any..."
    _Limit 15
Next
Sleep
Cls
Print "WOW! what was that!?"
Print
_Delay 1
Print "The Birth of Sierpinski Flies a Kite."
Print
_Delay 1
Print "Actually any symmetric object might dance around like that!"
Print
_Delay 1
Print "Maybe you have one to try?"

Sub drawKite (x, y, s, a)
    Line (x, y)-(x + s * Cos(_Pi(2) - a), (y - s) + s * Sin(_Pi(2) - a))
    Line (x, y)-(x + s * Cos(_Pi + a), (y - s) + s * Sin(_Pi + a))
    If s > 1 Then
        drawKite x + s * Cos(_Pi(2) - a), (y - s) + s * Sin(_Pi(2) - a), s / 2, a
        drawKite x + s * Cos(_Pi + a), (y - s) + s * Sin(_Pi + a), s / 2, a
    End If
End Sub

Sub drawKite2 (xx, yy, s, a)
    x = xx: y = yy
    x2 = x + 3 * s * Cos(_Pi(1 / 2) - a / 2): y2 = y + 3 * s * Sin(_Pi(1 / 2) - a / 2)
    x3 = x + 3 * s * Cos(_Pi(1 / 2) + a / 2): y3 = y + 3 * s * Sin(_Pi(1 / 2) + a / 2)
    SierLineTri x, y, x2, y2, x3, y3, 0
    If s > 10 Then
        drawKite2 x + 1 * s * Cos(_Pi(2) - a), (y - s) + 1 * s * Sin(_Pi(2) - a), s / 2, a
        drawKite2 x + 1 * s * Cos(_Pi + a), (y - s) + 1 * s * Sin(_Pi + a), s / 2, a
    End If
End Sub


Sub SierLineTri (x1, y1, x2, y2, x3, y3, depth)
    If depth = 0 Then 'draw out triangle if level 0
        Line (x1, y1)-(x2, y2)
        Line (x2, y2)-(x3, y3)
        Line (x1, y1)-(x3, y3)
    End If
    'find midpoints
    If x2 < x1 Then mx1 = (x1 - x2) / 2 + x2 Else mx1 = (x2 - x1) / 2 + x1
    If y2 < y1 Then my1 = (y1 - y2) / 2 + y2 Else my1 = (y2 - y1) / 2 + y1
    If x3 < x2 Then mx2 = (x2 - x3) / 2 + x3 Else mx2 = (x3 - x2) / 2 + x2
    If y3 < y2 Then my2 = (y2 - y3) / 2 + y3 Else my2 = (y3 - y2) / 2 + y2
    If x3 < x1 Then mx3 = (x1 - x3) / 2 + x3 Else mx3 = (x3 - x1) / 2 + x1
    If y3 < y1 Then my3 = (y1 - y3) / 2 + y3 Else my3 = (y3 - y1) / 2 + y1
    Line (mx1, my1)-(mx2, my2) '  'draw all inner triangles
    Line (mx2, my2)-(mx3, my3)
    Line (mx1, my1)-(mx3, my3)
    If depth < 4 Then 'not done so call me again
        SierLineTri x1, y1, mx1, my1, mx3, my3, depth + 1
        SierLineTri x2, y2, mx1, my1, mx2, my2, depth + 1
        SierLineTri x3, y3, mx3, my3, mx2, my2, depth + 1
    End If
End Sub