Would it make understanding graphics easier to follow, specially employing Sin, Cos and _Atan2?
Here I've converted Sin, Cos, _Atan2, DrawArc and ArrowTo to using Degree Units in the Call to the Sub and internalized all the radian conversions inside the Sub.
Here is main Demo:
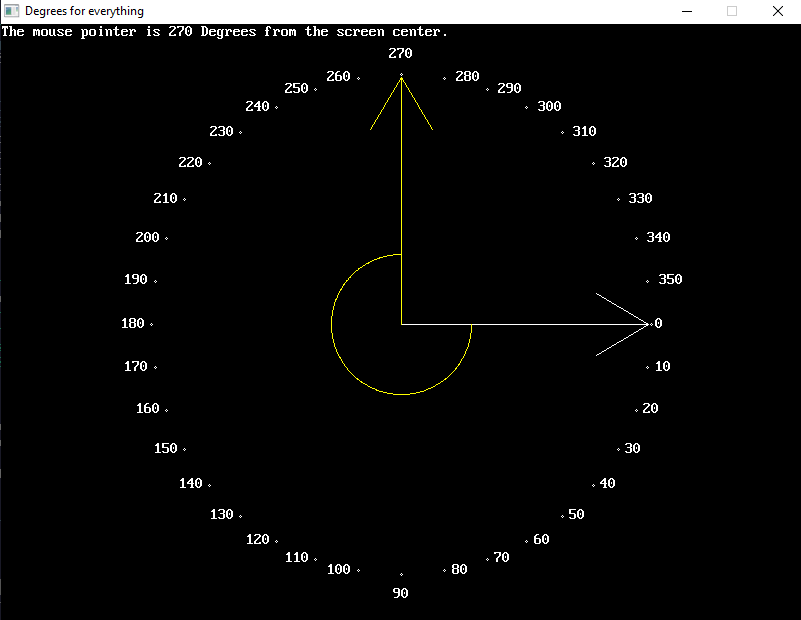
Here I've converted Sin, Cos, _Atan2, DrawArc and ArrowTo to using Degree Units in the Call to the Sub and internalized all the radian conversions inside the Sub.
Here is main Demo:
Code: (Select All)
' OK let's be rid on the confusion caused by Radians
' by using User Defined Functions SinD and CosD that take Degrees 0 to 360 for whole circle,
' and having replaced _Atan2 by returning an angle in Degrees between 2 points: DAtan2(baseX, baseY, angleToX, angleToY)
_Title "Degrees for everything" 'b+ 2022-10-12
Screen _NewImage(800, 600, 32) ' standard screen size 800 wide, 600 height for quick QB64 Demos with full color potential (the 32)
_ScreenMove 250, 50
cx = _Width / 2 ' middle of the screen point center x
cy = _Height / 2 ' center y
radius = 250 ' max is 300 for height 600
ArrowTo cx, cy, 0, radius - 3, &HFFFFFFFF
For degrees = 0 To 359 Step 10 ' go around a full circle in degrees in steps of 10 degrees
' calculate and draw points around the center of the screen
x = cx + radius * CosD(degrees) ' use CosD for x dimensions
y = cy + radius * SinD(degrees) ' use SinD for y dimensions
Circle (x, y), 1 ' draw bigger points than single pixel
' labeling the degree angles before or after the point ?
If x < cx Then Xoffset = -10 * Len(_Trim$(Str$(degrees))): YOffset = 0
If x > cx Then Xoffset = 4 * Len(_Trim$(Str$(degrees))): YOffset = 0
If x = cx Then
Xoffset = -4 * Len(_Trim$(Str$(degrees)))
If y > cy Then YOffset = 20 Else YOffset = -20
End If
_PrintString (x + Xoffset, y - 8 + YOffset), _Trim$(Str$(degrees))
Next
' save our compass dial to image
dial& = _NewImage(_Width, _Height, 32)
_PutImage , 0, dial& ' screen to dial image stored
' Getting use to seeing angles mouse makes to center of screen
Do
Cls
_PutImage , dial&, 0
While _MouseInput: Wend ' this checks where mouse is right now!
mx = _MouseX: my = _MouseY: mb1 = _MouseButton(1) ' left mouse down ' saves mouse status to common variable names
'lets's the angle in degrees the mouse is to the center of the screen
dAngle = DAtan2(cx, cy, mx, my)
Print "The mouse pointer is "; _Trim$(Str$(dAngle)); " Degrees from the screen center." ' then center point is first the mouse point is second
ArrowTo cx, cy, dAngle, radius - 3, &HFFFFFF00
drawArc cx, cy, 70, 0, dAngle, &HFFFFFF00
_Display ' stop the blinking
_Limit 60 ' only loop 60 times per second
Loop Until _KeyDown(27)
' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
CosD = Cos(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
SinD = Sin(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2) makes to a first point (x1, y1)
' Note this function uses whatever the default type is, better not be some Integer Type.
' Delta means change between 1 measure and another for example x2 - x1
deltaX = x2 - x1
deltaY = y2 - y1
' To find the angle point(x2, y2) makes to (x1, y1) in Degrees
' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
rtn = _R2D(_Atan2(deltaY, deltaX))
If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function
' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
Dim As Long x1, y1, x2, y2, x3, y3
Dim As Double rAngle
rAngle = _D2R(dAngle)
x1 = BaseX + lngth * Cos(rAngle)
y1 = BaseY + lngth * Sin(rAngle)
x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
Line (BaseX, BaseY)-(x1, y1), colr
Line (x1, y1)-(x2, y2), colr
Line (x1, y1)-(x3, y3), colr
End Sub
' use angles in degrees units instead of radians (converted inside sub)
Sub drawArc (xc, yc, radius, dStart, dMeasure, colr As _Unsigned Long)
' xc, yc Center for arc circle
' rStart is the Radian Start Angle, use _D2R for conversion from Degrees to Radians
' rMeasure is the measure of Arc in Radain units, use _D2R for conversion from Degrees to Radians
' Arc will start at rStart and go clockwise around for rMeasure Radians
Dim rStart, rMeasure, rEnd, stepper, a, x, y
rStart = _D2R(dStart)
rMeasure = _D2R(dMeasure)
rEnd = rStart + rMeasure
stepper = 1 / radius ' the bigger the radius the smaller the steps
For a = rStart To rEnd Step stepper
x = xc + radius * Cos(a)
y = yc + radius * Sin(a)
If a > rStart Then Line -(x, y), colr Else PSet (x, y), colr
Next
End Sub
b = b + ...