10-16-2022, 12:48 PM
(This post was last modified: 10-16-2022, 01:34 PM by bplus.
Edit Reason: Code was missing Poly Fill sub routine, want to keep all Degrees subs together
)
Hey let's bounce a ball inside some regular polygons!
Code: (Select All)
Option _Explicit
_Title "Bounce Ball Inside Polygon" 'b+ 2022-10-16
Screen _NewImage(800, 600, 32) ' standard screen size 800 wide, 600 height for quick QB64 Demos with full color potential (the 32)
_ScreenMove 250, 50
Randomize Timer
_PrintMode _KeepBackground
Type lineSegment
As Single x1, y1, x2, y2, dN ' 2 end points
End Type
' mod RegularPoly to save lines created by
Dim cx, cy, polyRadius, Dstart, SecDegrees, x1, y1, x2, y2 ' building container
Dim As _Unsigned Long PK
Dim As Long NLines, L, Container
cx = _Width / 2: cy = _Height / 2 + 40: polyRadius = 250: Dstart = 270
PK = _RGB32(0, 150, 85) ' minty green background out of bounds
startNewPoly:
NLines = Int(Rnd * 10) + 3
SecDegrees = 360 / NLines
ReDim Boundaries(1 To NLines) As lineSegment
Cls
x1 = cx + polyRadius * CosD(Dstart)
y1 = cy + polyRadius * SinD(Dstart)
For L = 1 To NLines
x2 = cx + polyRadius * CosD(Dstart + L * SecDegrees)
y2 = cy + polyRadius * SinD(Dstart + L * SecDegrees)
Line (x1, y1)-(x2, y2), PK ' back to first point
Boundaries(L).x1 = x1 ' save these line segment end points for containing the ball
Boundaries(L).y1 = y1
Boundaries(L).x2 = x2
Boundaries(L).y2 = y2
'if we take the midpoint of the two endpoints and draw a line to the center we have the normal angle of the line
' on the same side we want to keep the ball!
' midx = (x1+ x2)/2
' midy = (y1 + y2)/2
' the angle of the normal is! Aha!
Boundaries(L).dN = DAtan2((x1 + x2) / 2, (y1 + y2) / 2, cx, cy) ' angle from midpoint to center
' check angles midpoint is 22.5 degress less (for 8 sides) and going in opp direction
' Print Dstart + L * SecDegrees - 22.5 - 180, Boundaries(L).dN
x1 = x2: y1 = y2
Next
Paint (1, 1), PK, PK
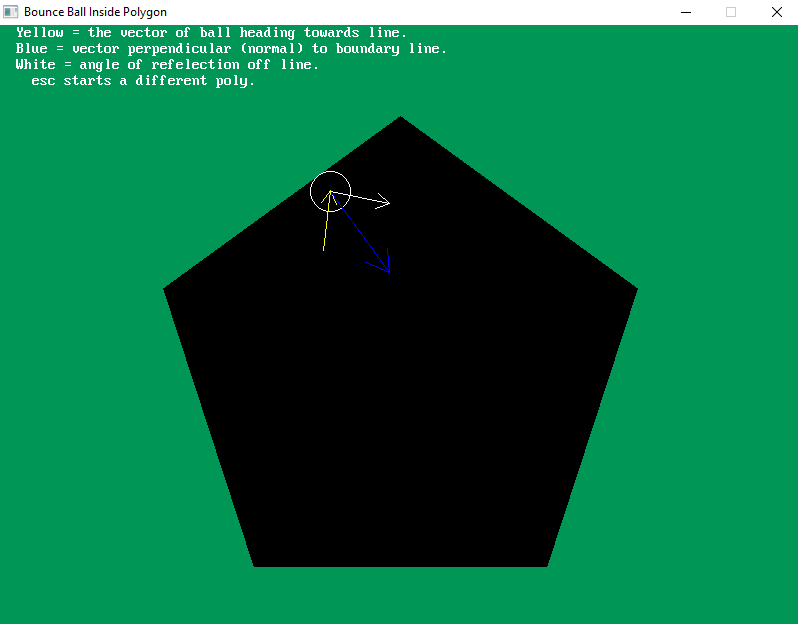
Print " Yellow = the vector of ball heading towards line."
Print " Blue = vector perpendicular (normal) to boundary line."
Print " White = angle of refelection off line."
Print " esc starts a different poly."
Container = _NewImage(_Width, _Height, 32)
_PutImage , 0, Container
Dim bx, by, ba, br, bspeed, hit, hitx1, hity1, hitx2, hity2, diff
bx = cx: by = cy: bspeed = 5
br = 20 ' make ball radius (br) at least 2* speed
ba = Rnd * 360 ' setup up ball in middle of screen/container random heading = ba (ball angle)
' ok just bounce ball around the polygon container
Do
_PutImage , Container, 0
Circle (bx, by), br ' draw ball then calc next loaction
bx = bx + bspeed * CosD(ba) ' test x, y is new ball position if dont run into wall
by = by + bspeed * SinD(ba)
For L = 1 To NLines ' did we hit any?
hit = lineIntersectCircle%(Boundaries(L).x1, Boundaries(L).y1, Boundaries(L).x2, Boundaries(L).y2, bx, by, br, hitx1, hity1, hitx2, hity2)
' probably should back it up before processing bounce
If hit Then ' rebound ball
Circle (bx, by), br
_Display
While hit ' back up circle
bx = bx + CosD(ba - 180)
by = by + SinD(ba - 180)
hit = lineIntersectCircle%(Boundaries(L).x1, Boundaries(L).y1, Boundaries(L).x2, Boundaries(L).y2, bx, by, br, hitx1, hity1, hitx2, hity2)
'Circle (bx, by), br
'_Display
Wend
_PutImage , Container, 0
Circle (bx, by), br
' Yellow arrow for incoming towards boundary (I reversed the head of arrow to compare to reflection angle)
ArrowTo bx + 3 * br * CosD(ba + 180), by + 3 * br * SinD(ba + 180), ba, 3 * br, &HFFFFFF00
' Blue Vector Perpendicular to plane
ArrowTo bx, by, Boundaries(L).dN, 5 * br, &HFF0000FF
' Reflected ball off line
diff = Boundaries(L).dN - ba + 180
ba = Boundaries(L).dN + diff ' >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> new direction
ArrowTo bx, by, ba, 3 * br, &HFFFFFFFF
_Display
_Delay 1
End If
Next
_Display
_Limit 30
Loop Until _KeyDown(27)
GoTo startNewPoly
' return 0 no Intersect, 1 = tangent 1 point touch, 2 = 2 point intersect
' if intersect returns point or points of intersect ix1, iy1, ix2, iy2
' intersect points are -999 if non existent ie no intersect or 2nd point when circle is tangent
Function lineIntersectCircle% (lx1, ly1, lx2, ly2, cx, cy, r, ix1, iy1, ix2, iy2)
Dim m, y0, A, B, C, D, x1, y1, x2, y2, ydist
'needs SUB slopeYintersect (X1, Y1, X2, Y2, slope, Yintercept)
If lx1 <> lx2 Then
slopeYintersect lx1, ly1, lx2, ly2, m, y0 ' Y0 otherwise know as y Intersect
' https://math.stackexchange.com/questions/228841/how-do-i-calculate-the-intersections-of-a-straight-line-and-a-circle
A = m ^ 2 + 1
B = 2 * (m * y0 - m * cy - cx)
C = cy ^ 2 - r ^ 2 + cx ^ 2 - 2 * y0 * cy + y0 ^ 2
D = B ^ 2 - 4 * A * C 'telling part of Quadratic formula = 0 then circle is tangent or > 0 then 2 intersect points
If D < 0 Then ' no intersection
ix1 = -999: iy1 = -999: ix2 = -999: iy2 = -999: lineIntersectCircle% = 0
ElseIf D = 0 Then ' one point tangent
x1 = (-B + Sqr(D)) / (2 * A)
y1 = m * x1 + y0
ix1 = x1: iy1 = y1: ix2 = -999: iy2 = -999: lineIntersectCircle% = 1
Else '2 points
x1 = (-B + Sqr(D)) / (2 * A): y1 = m * x1 + y0
x2 = (-B - Sqr(D)) / (2 * A): y2 = m * x2 + y0
ix1 = x1: iy1 = y1: ix2 = x2: iy2 = y2: lineIntersectCircle% = 2
End If
Else 'vertical line
If r = Abs(lx1 - cx) Then ' tangent
ix1 = lx1: iy1 = cy: ix2 = -999: iy2 = -999: lineIntersectCircle% = 1
ElseIf r < Abs(lx1 - cx) Then 'no intersect
ix1 = -999: iy1 = -999: ix2 = -999: iy2 = -999: lineIntersectCircle% = 0
Else '2 point intersect
ydist = Sqr(r ^ 2 - (lx1 - cx) ^ 2)
ix1 = lx1: iy1 = cy + ydist: ix2 = lx1: iy2 = cy - ydist: lineIntersectCircle% = 2
End If
End If
End Function
Sub slopeYintersect (X1, Y1, X2, Y2, slope, Yintercept) ' fix for when x1 = x2
slope = (Y2 - Y1) / (X2 - X1)
Yintercept = slope * (0 - X1) + Y1
End Sub
Sub RegularPolyFill (cx, cy, radius, nPoints, dStart, K As _Unsigned Long)
Dim secDegrees, p, x, y, lastX, lastY, startX, startY
secDegrees = 360 / nPoints
For p = 1 To nPoints
x = cx + radius * CosD(dStart + p * secDegrees)
y = cy + radius * SinD(dStart + p * secDegrees)
If p > 1 Then
TriFill cx, cy, lastX, lastY, x, y, K
Else
startX = x: startY = y
End If
lastX = x: lastY = y
Next
TriFill cx, cy, lastX, lastY, startX, startY, K ' back to first point
End Sub
Sub RegularPoly (cx, cy, radius, nPoints, dStart, K As _Unsigned Long)
Dim secDegrees, p, x, y, saveX, saveY
secDegrees = 360 / nPoints
For p = 1 To nPoints
x = cx + radius * CosD(dStart + p * secDegrees)
y = cy + radius * SinD(dStart + p * secDegrees)
If p = 1 Then PSet (x, y), K: saveX = x: saveY = y Else Line -(x, y), K
Next
Line -(saveX, saveY), K ' back to first point
End Sub
' use angles in degrees units instead of radians (converted inside sub)
Function CosD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
CosD = Cos(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function SinD (degrees)
' Note this function uses whatever the default type is, better not be some Integer Type.
SinD = Sin(_D2R(degrees))
End Function
' use angles in degrees units instead of radians (converted inside sub)
Function DAtan2 (x1, y1, x2, y2) ' The angle in degrees a 2nd point (x2, y2) makes to a first point (x1, y1)
' Note this function uses whatever the default type is, better not be some Integer Type.
' Delta means change between 1 measure and another for example x2 - x1
Dim deltaX, deltaY, rtn
deltaX = x2 - x1
deltaY = y2 - y1
' To find the angle point(x2, y2) makes to (x1, y1) in Degrees
' Take DegreeAngle = DAtan2(y2 - y1, x2 - x1)
rtn = _R2D(_Atan2(deltaY, deltaX))
If rtn < 0 Then DAtan2 = rtn + 360 Else DAtan2 = rtn
End Function
' use angles in degrees units instead of radians (converted inside sub)
Sub ArrowTo (BaseX As Long, BaseY As Long, dAngle As Double, lngth As Long, colr As _Unsigned Long)
Dim As Long x1, y1, x2, y2, x3, y3
Dim As Double rAngle
rAngle = _D2R(dAngle)
x1 = BaseX + lngth * Cos(rAngle)
y1 = BaseY + lngth * Sin(rAngle)
x2 = BaseX + .8 * lngth * Cos(rAngle - _Pi(.05))
y2 = BaseY + .8 * lngth * Sin(rAngle - _Pi(.05))
x3 = BaseX + .8 * lngth * Cos(rAngle + _Pi(.05))
y3 = BaseY + .8 * lngth * Sin(rAngle + _Pi(.05))
Line (BaseX, BaseY)-(x1, y1), colr
Line (x1, y1)-(x2, y2), colr
Line (x1, y1)-(x3, y3), colr
End Sub
' use angles in degrees units instead of radians (converted inside sub)
Sub drawArc (xc, yc, radius, dStart, dMeasure, colr As _Unsigned Long)
' xc, yc Center for arc circle
' rStart is the Radian Start Angle, use _D2R for conversion from Degrees to Radians
' rMeasure is the measure of Arc in Radain units, use _D2R for conversion from Degrees to Radians
' Arc will start at rStart and go clockwise around for rMeasure Radians
Dim rStart, rMeasure, rEnd, stepper, a, x, y
rStart = _D2R(dStart)
rMeasure = _D2R(dMeasure)
rEnd = rStart + rMeasure
stepper = 1 / radius ' the bigger the radius the smaller the steps
For a = rStart To rEnd Step stepper
x = xc + radius * Cos(a)
y = yc + radius * Sin(a)
If a > rStart Then Line -(x, y), colr Else PSet (x, y), colr
Next
End Sub
'' BEST saves dest and optimized with Static a& and alpha colors work better
'2019-12-16 fix by Steve saves some time with STATIC and saves and restores last dest
Sub TriFill (x1, y1, x2, y2, x3, y3, K As _Unsigned Long) ' 2022-10-13 changed name
Dim D As Long
Static a&
D = _Dest
If a& = 0 Then a& = _NewImage(1, 1, 32)
_Dest a&
_DontBlend a& ' '<<<< new 2019-12-16 fix
PSet (0, 0), K
_Blend a& '<<<< new 2019-12-16 fix
_Dest D
_MapTriangle _Seamless(0, 0)-(0, 0)-(0, 0), a& To(x1, y1)-(x2, y2)-(x3, y3)
End Sub
b = b + ...