I get this:
'45 /2 = 22.5
'sin(_d2r(22.5) = a/5 ' Update: actually (1/2 of a) /5 = sin(22.5 degrees)
Print "a ="; 2 * (5 * Sin(_D2R(22.5))) ' 3.8268...
The only way you might avoid a trig table is if you can somehow use the fact that 22.5 is 1/3 of 67.5 the base angles of the iso tri.
My trig not that good.
Here it is illustrated in QB64pe:
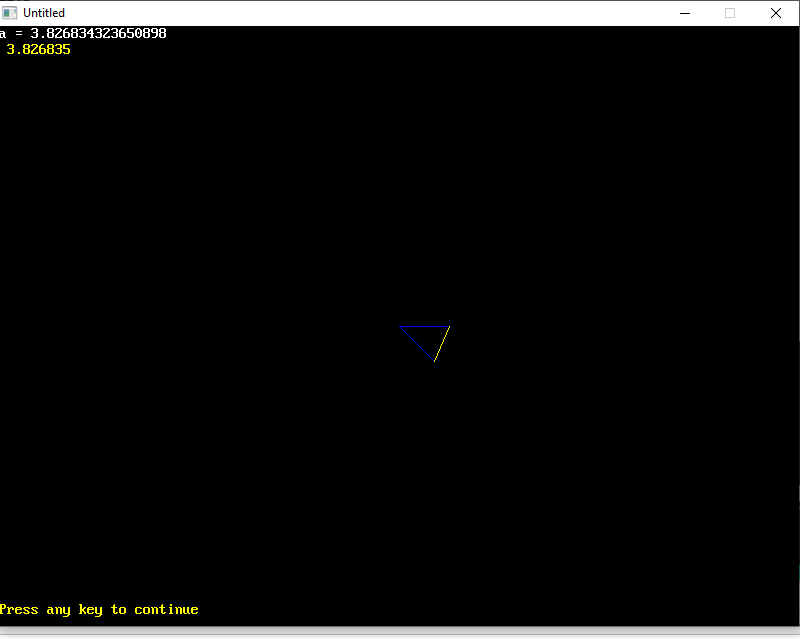
'45 /2 = 22.5
'sin(_d2r(22.5) = a/5 ' Update: actually (1/2 of a) /5 = sin(22.5 degrees)
Print "a ="; 2 * (5 * Sin(_D2R(22.5))) ' 3.8268...
The only way you might avoid a trig table is if you can somehow use the fact that 22.5 is 1/3 of 67.5 the base angles of the iso tri.
My trig not that good.
Here it is illustrated in QB64pe:
Code: (Select All)
Screen _NewImage(800, 600, 32)
'45 /2 = 22.5
'sin(_d2r(22.5) = a/5
Print "a ="; 2 * (5 * Sin(_D2R(22.5))) ' 3.8268...
'draw scale model
xc = 400: yc = 300 ' center of screen
scale = 10
radius = 5 * scale
x1 = xc + radius * Cos(0): y1 = yc + radius * Sin(0)
x2 = xc + radius * Cos(_D2R(45)): y2 = yc + radius * Sin(_D2R(45))
Line (xc, yc)-(x1, y1), &HFF0000FF
Line (xc, yc)-(x2, y2), &HFF0000FF
Color &HFFFFFF00
Line (x1, y1)-(x2, y2),
dist = Sqr((x1 - x2) ^ 2 + (y1 - y2) ^ 2)
Print dist / scale
b = b + ...



