Login

Space_Ghost · 07-09-2023, 03:58 AM

Does QB64pe have the capability for Big Integers?

Below I pasted python (P3) code that calculates the first 5,000 Fibonacci numbers as shown. Takes about 1 second. It automatically uses Big Integers with no adjustment.

Can we do something similar with QB64pe? I would guess there is at least one or more ways to run a similar calculation. Thanks in advance !!!

Python Code for Fibonacci Sequence
def fibIter(n):
if n < 2:
return n
fibPrev = 1
fib = 1
for _ in range(2, n):
fibPrev, fib = fib, fib + fibPrev
return fib

for i in range(0, 5000):
print(fibIter(i))

This is the 5000th Fibonacci Number (it has 1,045 digits) I skipped 1 to 4,999.
2397334346100631452333336800023778743396400988090212332865227234032387117767626167465060795065595580850691237390963845987165478074085124644348902530685083246709423858342692329718110162972268152200857232686119638781547238020078362945470777668711057069618425746387920931255084621360135655698456629322111614827324455767748623844363426260372374195153577101298837831208580530677289982029527164306876024342838547454228388796380077029917639469963653048076473269452943584037848773158456736367057460079075603072996653089318046279296240100777360367200040226807430924334616931577257195085793060133817911514540227011756335999604550121968663793604830945238116686325506344893928776515696088851468818023735825546502317562957459506612704850760351077006532507519813600498603205937022956740021970327599548184626715032015801445754074519753924901317605013561516613650173445818028242577356369143977719495739428130191089993769093308407443558168431535751910046557480949313497996285124526992631353143367314930548703966553707195171094152730704138121243470432644848607501

TerryRitchie · 07-09-2023, 05:00 AM

Here is the function converted to QB64 using an unsigned _INTEGER64. Of course it breaks down at the upper limit of _INTEGER64. Interesting coding challenge. Thoughts anyone?

Code: (Select All)



FOR i = 1 TO 100

    _LIMIT 10

    PRINT fibIter(i)

NEXT i





FUNCTION fibIter~&& (n)

    IF n < 2 THEN

        fibIter = n

    ELSE

        fibPrev = 1

        fib = 1

        FOR i = 2 TO n - 1

            fibPrevTemp = fib

            fib = fib + fibPrev

            fibPrev = fibPrevTemp

        NEXT i

        fibIter = fib

    END IF

END FUNCTION

Jack · 07-09-2023, 06:21 AM

Space_Ghost
what OS are you using?
if you are using Windows x64 then here's TerryRitchie's example converted to use LibTomath https://staging.qb64phoenix.com/showthread.php?tid=31

Code: (Select All)

  
_Title "Fibonacci"
 
$Console:Only
_Dest _Console
 
'$include: 'LibTomMath.bi'
 
Dim As mp_int fibIter
Dim As Long i, ok
Dim As Double t
t = Timer(.0001)
If mp_init(fibIter) <> 0 Then Print "failed to initialize"
 
For i = 1 To 5000 - 1
    fibonacci fibIter, i
    Print i, mp_str(fibIter, 10)
Next i
t = Timer(.0001) - t
Print "elapsed time - "; t; " seconds"
mp_clear fibIter
 
Sub fibonacci (f As mp_int, n As Long)
    Dim As Long i
    Dim As mp_int fib, fibPrev, fibPrevTemp
    If mp_init(fib) <> 0 Then Print "failed to initialize"
    If mp_init(fibPrev) <> 0 Then Print "failed to initialize"
    If mp_init(fibPrevTemp) <> 0 Then Print "failed to initialize"
    If n < 2 Then
        mp_set_i32 f, n
    Else
        mp_set_i32 fibPrev, 1
        mp_set_i32 fib, 1
        For i = 2 To n - 1
            ok = mp_copy(fib, fibPrevTemp)
            ok = mp_add&(fibPrev, fib, fib)
            ok = mp_copy(fibPrevTemp, fibPrev)
        Next i
        ok = mp_copy(fib, f)
        mp_clear fibPrevTemp
        mp_clear fibPrev
        mp_clear fib
    End If
End Sub
 
'$include: 'LibTomMath.bm'

LibTomMath.bi (Size: 12.99 KB / Downloads: 66)

.bm

LibTomMath.bm (Size: 636 bytes / Downloads: 60)

.zip

libtommath.zip (Size: 59.37 KB / Downloads: 26)

Jack · 07-09-2023, 06:35 AM

also for Windows x64 you can use pari https://staging.qb64phoenix.com/showthread.php?tid=536

Code: (Select All)

  
_Title "libpari-fib-demo"
$Console:Only
_Dest _Console
 
Declare Dynamic Library "libpari"
    Sub pari_init (ByVal parisize~&&, Byval maxprime~&&)
    Sub pari_close ()
    Sub pari_print_version ()
    Function setdefault~&& (s As String, v As String, Byval flag&&)
    Function strtoGENstr~&& (s As String)
    Function setrealprecision&& (ByVal n&&, prec&&)
    Function GENtostr$ (ByVal x~&&)
    Function geval~&& (ByVal x~&&)
    Sub outmat (ByVal x~&&)
    Function gp_input~&& ()
    Function stoi~&& (ByVal x&&)
    Function abscmpiu& (ByVal x~&&, Byval y As _Unsigned _Integer64)
    Function abscmpui& (ByVal x As _Unsigned _Integer64, Byval y~&&)
    Function absequaliu& (ByVal x~&&, Byval y As _Unsigned _Integer64)
    Function gequal& (ByVal x~&&, Byval y~&&)
    Function gcmp& (ByVal x~&&, Byval y~&&)
End Declare
 
Dim As _Unsigned _Integer64 a, b, c, d, e, f
Dim As String s1, s2, s3
Dim As _Integer64 flag, prec
 
pari_init 80000000, 500000
'pari_print_version
Print
 
s1 = "fibonacci(5000)" + Chr$(0)
a = strtoGENstr(s1) 'convert to GEN string
b = geval(a) 'eval the string in a
'outmat b
s3 = GENtostr(b)
Print "fibonacci(5000) = "; s3
 
pari_close

david_uwi · 07-09-2023, 07:14 AM

Using arrays and carries is quite quick... Might be even quicker using LONG integers in the array.
There is also some problems with type conversions.
Does INTEGER to LONG conversion slow things down?
Anyway it is much quicker than using strings.

Code: (Select All)
Cls

Dim a(30000) As Integer, b(30000) As Integer

DefLng F-I

DefInt J-N

Input "input the fibonacci number to calculate"; fmax

tt = Timer

b(1) = 1: n = 1

For i = 1 To (fmax + 1) \ 2

    For j = 1 To n

        b(j) = a(j) + b(j) + jc

        If b(j) > 9999 Then b(j) = b(j) - 10000: jc = 1 Else jc = 0

    Next j

    If jc = 1 Then n = n + 1: b(n) = 1: jc = 0

    For j = 1 To n

        a(j) = a(j) + b(j) + jc

        If a(j) > 9999 Then a(j) = a(j) - 10000: jc = 1 Else jc = 0

    Next j

    If jc = 1 Then n = n + 1: a(n) = 1: jc = 0

Next i

For j = n To 1 Step -1

    If fmax Mod 2 = 0 Then

        If j = n Then t$ = LTrim$(Str$(a(j))) Else t$ = Right$("0000" + LTrim$(Str$(a(j))), 4)

        Print Using "&"; t$;

    End If

    If fmax Mod 2 = 1 Then

        If j = n Then t$ = LTrim$(Str$(b(j))) Else t$ = Right$("0000" + LTrim$(Str$(b(j))), 4)

        Print Using "&"; t$;

    End If

Next j

Print: Print "number of digits = ";

If fmax Mod 2 = 1 Then Print (n - 1) * 4 + Len(LTrim$(Str$(a(n))))

If fmax Mod 2 = 0 Then Print (n - 1) * 4 + Len(LTrim$(Str$(b(n))))

Print "TIME TAKEN= "; Timer - tt; "SECONDS"

End

Space_Ghost · 07-09-2023, 07:55 AM

Thank you to Terry, Jack, and David !!!

Jack, per your question, I am using:

Windows 11 Pro, x64-based PC
Version 10.0 Build 22621
Intel Core i7 w/6 cores and 12 Logical Processors
16 GB RAM

It is amazing how fast you all came up with options. I am fading fast right now...but will try all of these in the a.m.

Again, thanks for the great and professional feedback! This is a very interesting and useful item if we can get it to work in a general manner.

Cheers

**SMcNeill** · 07-09-2023, 02:20 PM

Code: (Select All)

 Screen _NewImage(1280, 720, 32)
Limit = 10000
Print "Fib"; Limit; "="
last2$ = "0"
last$ = "1"
time## = Timer
For i = 1 To Limit - 2
    result$ = StringAdd(last$, last2$)
    last2$ = last$
    last$ = result$
Next
Print result$
Print Using "###.### seconds to run."; Timer - time##
 
End
 
Function StringAdd$ (tempa$, tempb$)
    a$ = tempa$: b$ = tempb$ 'don't alter our original numbers
    Dim As _Unsigned _Integer64 a, b, c, carryover 'to hold our values
 
    'first fix the numbers to notmalize their lengths
    FixNumbers a$, b$
    'find the signs and strip them off
    If Left$(a$, 1) = "-" Then sa$ = "-": a$ = Mid$(a$, 2) Else sa$ = " "
    If Left$(b$, 1) = "-" Then sb$ = "-": b$ = Mid$(b$, 2) Else sb$ = " "
    'find the decimal position
    dp = InStr(a$, ".")
    If dp > 0 Then 'remove the decimal place from our numbers.  We can put it back later, in its proper position
        righta$ = Mid$(a$, dp + 1)
        rightb$ = Mid$(b$, dp + 1)
        a$ = Left$(a$, dp - 1) + righta$
        b$ = Left$(b$, dp - 1) + rightb$
    End If
    'our strings are now nothing but numbers with no signs and no decimals to deal with.  Let's start adding!
    'are we adding or really subtracting?
 
    If sa$ <> sb$ Then 'we're subtracting the two values if the signs aren't the same.
        Select Case a$
            Case Is < b$: s$ = sb$: Swap a$, b$ 'our sign is going to be determiined by b$
            Case Is = b$ 'if the two values are the same and are subtracting, our result is zero!
                StringAdd$ = "0" 'How easy was that?
                Exit Function
            Case Else: s$ = sa$ 'our sign is determined by a$
        End Select
        Do
            lb = Len(b$)
            a = Val(Right$(a$, 18)): a$ = Left$(a$, Len(a$) - 18)
            b = Val(Right$(b$, 18)): b$ = Left$(b$, Len(b$) - 18)
            If borrow Then b = b + 1~&& 'in case we had to borrow a digit for the last subtraction
            If a < b Then
                If lb < 18 Then a = a + 10 ^ lb Else a = a + 10 ^ 18
                borrow = -1
            Else
                borrow = 0
            End If
            c = a - b
            temp$ = _Trim$(Str$(c))
            answer$ = String$(18 - Len(temp$), "0") + temp$ + answer$
        Loop Until Len(a$) = 0
        'remove leading 0's
        Do Until Left$(answer$, 1) <> "0"
            answer$ = Mid$(answer$, 2)
        Loop
        'remember to add in the decimal place before finished
        dp = Len(righta$)
        If dp > 0 Then
            answer$ = Left$(answer$, Len(answer$) - dp) + "." + Right$(answer$, dp)
        End If
        StringAdd$ = s$ + answer$
        Exit Function
    End If
 
    Do
        a1$ = Right$(a$, 18)
        b1$ = Right$(b$, 18)
        a = Val(Right$(a$, 18)): a$ = Left$(a$, Len(a$) - 18)
        b = Val(Right$(b$, 18)): b$ = Left$(b$, Len(b$) - 18)
        c = a + b + carryover
        temp$ = _Trim$(Str$(c))
        If Len(temp$) > 18 Then 'see if we have an answer that is more than 18 digits
            temp$ = Right$(temp$, 18) 'keep 18 digits
            carryover = 1 'store one for carry over
        Else
            carryover = 0 'no carryover
        End If
        answer$ = String$(18 - Len(temp$), "0") + temp$ + answer$
    Loop Until Len(a$) = 0
    If carryover Then answer$ = "1" + answer$
    'remember to add in the decimal place before finished
    dp = Len(righta$)
    If dp > 0 Then
        answer$ = Left$(answer$, Len(answer$) - dp) + "." + Right$(answer$, dp)
    End If
    'remove leading 0's
    Do Until Left$(answer$, 1) <> "0"
        answer$ = Mid$(answer$, 2)
    Loop
    StringAdd$ = sa$ + answer$
End Function
 
Function StringSubtract$ (tempa$, tempb$)
    a$ = tempa$: b$ = tempb$
    FixNumbers a$, b$
    If Left$(b$, 1) = "-" Then b$ = Mid$(b$, 2) Else b$ = "-" + b$
    StringSubtract$ = StringAdd$(a$, b$)
End Function
 
 
Sub FixNumbers (a$, b$)
    'first remove scientific notation and spaces from both
    a$ = _Trim$(N2S$(a$)): b$ = _Trim$(N2S$(b$))
    'then find the decimal position for both and normalize the expressions
    d1 = InStr(a$, "."): d2 = InStr(b$, ".")
    If d1 <> 0 Then 'break down the left and right side of the decimal point for ease of processing  (this is a$)
        lefta$ = Left$(a$, d1 - 1)
        righta$ = Mid$(a$, d1)
    Else
        lefta$ = a$
    End If
    If d2 <> 0 Then 'break down the left and right side of the decimal point for ease of processing  (this is b$)
        leftb$ = Left$(b$, d2 - 1)
        rightb$ = Mid$(b$, d2)
    Else
        leftb$ = b$
    End If
 
    'normalize the right side of our expressions
    l1 = Len(righta$): l2 = Len(rightb$)
    If l1 < l2 Then
        addzero = l2 - l1
        If l1 = 0 Then righta$ = ".": addzero = addzero - 1
        righta$ = righta$ + String$(addzero, "0")
    ElseIf l1 > l2 Then
        addzero = l1 - l2
        'If l2 = 0 Then rightb$ = ".": addzero = addzero - 1
        rightb$ = rightb$ + String$(addzero, "0")
    End If
 
 
 
    'strip off any plus/minus signs from the two numbers.
    If Left$(lefta$, 1) = "-" Then signa$ = "-": lefta$ = Mid$(lefta$, 2)
    If Left$(leftb$, 1) = "-" Then signb$ = "-": leftb$ = Mid$(leftb$, 2)
    If Left$(lefta$, 1) = "+" Then signa$ = "": lefta$ = Mid$(lefta$, 2)
    If Left$(leftb$, 1) = "+" Then signb$ = "": leftb$ = Mid$(leftb$, 2)
    'normalize the left side of our expressions
    l1 = Len(lefta$): l2 = Len(leftb$)
    If l1 < l2 Then
        addzero = l2 - l1
        lefta$ = String$(addzero, "0") + lefta$
    ElseIf l1 > l2 Then
        addzero = l1 - l2
        leftb$ = String$(addzero, "0") + leftb$
    End If
    'and then put it all together
    a$ = signa$ + lefta$ + righta$
    b$ = signb$ + leftb$ + rightb$
End Sub
 
 
 
 
 
Function N2S$ (exp$) 'scientific Notation to String
 
    t$ = LTrim$(RTrim$(exp$))
    If Left$(t$, 1) = "-" Or Left$(t$, 1) = "N" Then sign$ = "-": t$ = Mid$(t$, 2)
 
    dp = InStr(t$, "D+"): dm = InStr(t$, "D-")
    ep = InStr(t$, "E+"): em = InStr(t$, "E-")
    check1 = Sgn(dp) + Sgn(dm) + Sgn(ep) + Sgn(em)
    If check1 < 1 Or check1 > 1 Then N2S = exp$: Exit Function 'If no scientic notation is found, or if we find more than 1 type, it's not SN!
 
    Select Case l 'l now tells us where the SN starts at.
        Case Is < dp: l = dp
        Case Is < dm: l = dm
        Case Is < ep: l = ep
        Case Is < em: l = em
    End Select
 
    l$ = Left$(t$, l - 1) 'The left of the SN
    r$ = Mid$(t$, l + 1): r&& = Val(r$) 'The right of the SN, turned into a workable long
 
 
    If InStr(l$, ".") Then 'Location of the decimal, if any
        If r&& > 0 Then
            r&& = r&& - Len(l$) + 2
        Else
            r&& = r&& + 1
        End If
        l$ = Left$(l$, 1) + Mid$(l$, 3)
    End If
 
    Select Case r&&
        Case 0 'what the heck? We solved it already?
            'l$ = l$
        Case Is < 0
            For i = 1 To -r&&
                l$ = "0" + l$
            Next
            l$ = "0." + l$
        Case Else
            For i = 1 To r&&
                l$ = l$ + "0"
            Next
    End Select
 
    N2S$ = sign$ + l$
End Function
 
 
Function DWD$ (exp$) 'Deal With Duplicates
    'To deal with duplicate operators in our code.
    'Such as --  becomes a +
    '++ becomes a +
    '+- becomes a -
    '-+ becomes a -
    t$ = exp$
    Do
        bad = 0
        Do
            l = InStr(t$, "++")
            If l Then t$ = Left$(t$, l - 1) + "+" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
        Do
            l = InStr(t$, "+-")
            If l Then t$ = Left$(t$, l - 1) + "-" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
        Do
            l = InStr(t$, "-+")
            If l Then t$ = Left$(t$, l - 1) + "-" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
        Do
            l = InStr(t$, "--")
            If l Then t$ = Left$(t$, l - 1) + "+" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
    Loop Until Not bad
    DWD$ = t$
End Function

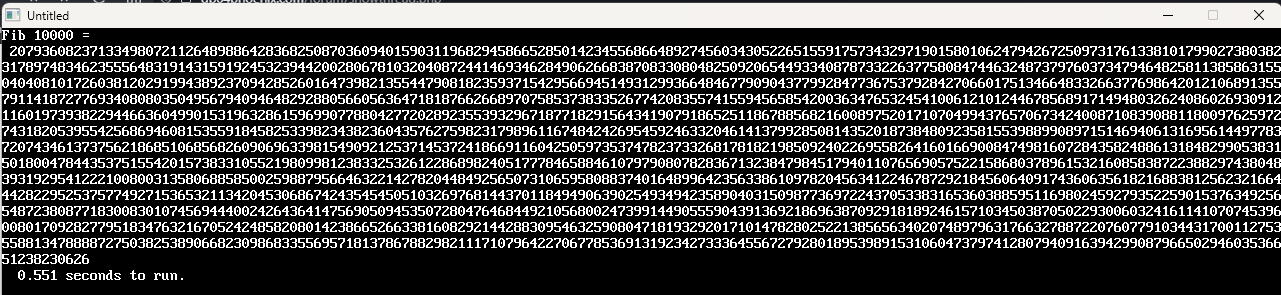
Filename: fib10000.png
Size: 41.23 KB
07-09-2023, 02:20 PM

TerryRitchie · 07-09-2023, 02:25 PM

(07-09-2023, 02:20 PM)SMcNeill Wrote:

Code: (Select All)

 Screen _NewImage(1280, 720, 32)
Limit = 10000
Print "Fib"; Limit; "="
last2$ = "0"
last$ = "1"
time## = Timer
For i = 1 To Limit - 2
    result$ = StringAdd(last$, last2$)
    last2$ = last$
    last$ = result$
Next
Print result$
Print Using "###.### seconds to run."; Timer - time##
 
End
 
Function StringAdd$ (tempa$, tempb$)
    a$ = tempa$: b$ = tempb$ 'don't alter our original numbers
    Dim As _Unsigned _Integer64 a, b, c, carryover 'to hold our values
 
    'first fix the numbers to notmalize their lengths
    FixNumbers a$, b$
    'find the signs and strip them off
    If Left$(a$, 1) = "-" Then sa$ = "-": a$ = Mid$(a$, 2) Else sa$ = " "
    If Left$(b$, 1) = "-" Then sb$ = "-": b$ = Mid$(b$, 2) Else sb$ = " "
    'find the decimal position
    dp = InStr(a$, ".")
    If dp > 0 Then 'remove the decimal place from our numbers.  We can put it back later, in its proper position
        righta$ = Mid$(a$, dp + 1)
        rightb$ = Mid$(b$, dp + 1)
        a$ = Left$(a$, dp - 1) + righta$
        b$ = Left$(b$, dp - 1) + rightb$
    End If
    'our strings are now nothing but numbers with no signs and no decimals to deal with.  Let's start adding!
    'are we adding or really subtracting?
 
    If sa$ <> sb$ Then 'we're subtracting the two values if the signs aren't the same.
        Select Case a$
            Case Is < b$: s$ = sb$: Swap a$, b$ 'our sign is going to be determiined by b$
            Case Is = b$ 'if the two values are the same and are subtracting, our result is zero!
                StringAdd$ = "0" 'How easy was that?
                Exit Function
            Case Else: s$ = sa$ 'our sign is determined by a$
        End Select
        Do
            lb = Len(b$)
            a = Val(Right$(a$, 18)): a$ = Left$(a$, Len(a$) - 18)
            b = Val(Right$(b$, 18)): b$ = Left$(b$, Len(b$) - 18)
            If borrow Then b = b + 1~&& 'in case we had to borrow a digit for the last subtraction
            If a < b Then
                If lb < 18 Then a = a + 10 ^ lb Else a = a + 10 ^ 18
                borrow = -1
            Else
                borrow = 0
            End If
            c = a - b
            temp$ = _Trim$(Str$(c))
            answer$ = String$(18 - Len(temp$), "0") + temp$ + answer$
        Loop Until Len(a$) = 0
        'remove leading 0's
        Do Until Left$(answer$, 1) <> "0"
            answer$ = Mid$(answer$, 2)
        Loop
        'remember to add in the decimal place before finished
        dp = Len(righta$)
        If dp > 0 Then
            answer$ = Left$(answer$, Len(answer$) - dp) + "." + Right$(answer$, dp)
        End If
        StringAdd$ = s$ + answer$
        Exit Function
    End If
 
    Do
        a1$ = Right$(a$, 18)
        b1$ = Right$(b$, 18)
        a = Val(Right$(a$, 18)): a$ = Left$(a$, Len(a$) - 18)
        b = Val(Right$(b$, 18)): b$ = Left$(b$, Len(b$) - 18)
        c = a + b + carryover
        temp$ = _Trim$(Str$(c))
        If Len(temp$) > 18 Then 'see if we have an answer that is more than 18 digits
            temp$ = Right$(temp$, 18) 'keep 18 digits
            carryover = 1 'store one for carry over
        Else
            carryover = 0 'no carryover
        End If
        answer$ = String$(18 - Len(temp$), "0") + temp$ + answer$
    Loop Until Len(a$) = 0
    If carryover Then answer$ = "1" + answer$
    'remember to add in the decimal place before finished
    dp = Len(righta$)
    If dp > 0 Then
        answer$ = Left$(answer$, Len(answer$) - dp) + "." + Right$(answer$, dp)
    End If
    'remove leading 0's
    Do Until Left$(answer$, 1) <> "0"
        answer$ = Mid$(answer$, 2)
    Loop
    StringAdd$ = sa$ + answer$
End Function
 
Function StringSubtract$ (tempa$, tempb$)
    a$ = tempa$: b$ = tempb$
    FixNumbers a$, b$
    If Left$(b$, 1) = "-" Then b$ = Mid$(b$, 2) Else b$ = "-" + b$
    StringSubtract$ = StringAdd$(a$, b$)
End Function
 
 
Sub FixNumbers (a$, b$)
    'first remove scientific notation and spaces from both
    a$ = _Trim$(N2S$(a$)): b$ = _Trim$(N2S$(b$))
    'then find the decimal position for both and normalize the expressions
    d1 = InStr(a$, "."): d2 = InStr(b$, ".")
    If d1 <> 0 Then 'break down the left and right side of the decimal point for ease of processing  (this is a$)
        lefta$ = Left$(a$, d1 - 1)
        righta$ = Mid$(a$, d1)
    Else
        lefta$ = a$
    End If
    If d2 <> 0 Then 'break down the left and right side of the decimal point for ease of processing  (this is b$)
        leftb$ = Left$(b$, d2 - 1)
        rightb$ = Mid$(b$, d2)
    Else
        leftb$ = b$
    End If
 
    'normalize the right side of our expressions
    l1 = Len(righta$): l2 = Len(rightb$)
    If l1 < l2 Then
        addzero = l2 - l1
        If l1 = 0 Then righta$ = ".": addzero = addzero - 1
        righta$ = righta$ + String$(addzero, "0")
    ElseIf l1 > l2 Then
        addzero = l1 - l2
        'If l2 = 0 Then rightb$ = ".": addzero = addzero - 1
        rightb$ = rightb$ + String$(addzero, "0")
    End If
 
 
 
    'strip off any plus/minus signs from the two numbers.
    If Left$(lefta$, 1) = "-" Then signa$ = "-": lefta$ = Mid$(lefta$, 2)
    If Left$(leftb$, 1) = "-" Then signb$ = "-": leftb$ = Mid$(leftb$, 2)
    If Left$(lefta$, 1) = "+" Then signa$ = "": lefta$ = Mid$(lefta$, 2)
    If Left$(leftb$, 1) = "+" Then signb$ = "": leftb$ = Mid$(leftb$, 2)
    'normalize the left side of our expressions
    l1 = Len(lefta$): l2 = Len(leftb$)
    If l1 < l2 Then
        addzero = l2 - l1
        lefta$ = String$(addzero, "0") + lefta$
    ElseIf l1 > l2 Then
        addzero = l1 - l2
        leftb$ = String$(addzero, "0") + leftb$
    End If
    'and then put it all together
    a$ = signa$ + lefta$ + righta$
    b$ = signb$ + leftb$ + rightb$
End Sub
 
 
 
 
 
Function N2S$ (exp$) 'scientific Notation to String
 
    t$ = LTrim$(RTrim$(exp$))
    If Left$(t$, 1) = "-" Or Left$(t$, 1) = "N" Then sign$ = "-": t$ = Mid$(t$, 2)
 
    dp = InStr(t$, "D+"): dm = InStr(t$, "D-")
    ep = InStr(t$, "E+"): em = InStr(t$, "E-")
    check1 = Sgn(dp) + Sgn(dm) + Sgn(ep) + Sgn(em)
    If check1 < 1 Or check1 > 1 Then N2S = exp$: Exit Function 'If no scientic notation is found, or if we find more than 1 type, it's not SN!
 
    Select Case l 'l now tells us where the SN starts at.
        Case Is < dp: l = dp
        Case Is < dm: l = dm
        Case Is < ep: l = ep
        Case Is < em: l = em
    End Select
 
    l$ = Left$(t$, l - 1) 'The left of the SN
    r$ = Mid$(t$, l + 1): r&& = Val(r$) 'The right of the SN, turned into a workable long
 
 
    If InStr(l$, ".") Then 'Location of the decimal, if any
        If r&& > 0 Then
            r&& = r&& - Len(l$) + 2
        Else
            r&& = r&& + 1
        End If
        l$ = Left$(l$, 1) + Mid$(l$, 3)
    End If
 
    Select Case r&&
        Case 0 'what the heck? We solved it already?
            'l$ = l$
        Case Is < 0
            For i = 1 To -r&&
                l$ = "0" + l$
            Next
            l$ = "0." + l$
        Case Else
            For i = 1 To r&&
                l$ = l$ + "0"
            Next
    End Select
 
    N2S$ = sign$ + l$
End Function
 
 
Function DWD$ (exp$) 'Deal With Duplicates
    'To deal with duplicate operators in our code.
    'Such as --  becomes a +
    '++ becomes a +
    '+- becomes a -
    '-+ becomes a -
    t$ = exp$
    Do
        bad = 0
        Do
            l = InStr(t$, "++")
            If l Then t$ = Left$(t$, l - 1) + "+" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
        Do
            l = InStr(t$, "+-")
            If l Then t$ = Left$(t$, l - 1) + "-" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
        Do
            l = InStr(t$, "-+")
            If l Then t$ = Left$(t$, l - 1) + "-" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
        Do
            l = InStr(t$, "--")
            If l Then t$ = Left$(t$, l - 1) + "+" + Mid$(t$, l + 2): bad = -1
        Loop Until l = 0
    Loop Until Not bad
    DWD$ = t$
End Function

Holy cow that's fast!

**SMcNeill** · 07-09-2023, 02:27 PM

(07-09-2023, 02:25 PM)TerryRitchie Wrote: Holy cow that's fast!

Not as fast as I'd like as it's all string math, but it's about as fast as you're going to get a string math routine to work for you, without direct memory manipulation. Wink

Space_Ghost · 07-09-2023, 03:56 PM

(07-09-2023, 02:27 PM)SMcNeill Wrote:
(07-09-2023, 02:25 PM)TerryRitchie Wrote: Holy cow that's fast!

Not as fast as I'd like as it's all string math, but it's about as fast as you're going to get a string math routine to work for you, without direct memory manipulation.

This is just insane! Amazing code Steve!
Greatly appreciate you sharing this and I have already learned quite a bit just looking at the code this a.m.
Cheers.

Login
Username/Email:
Password:	Lost Password?
	Remember me